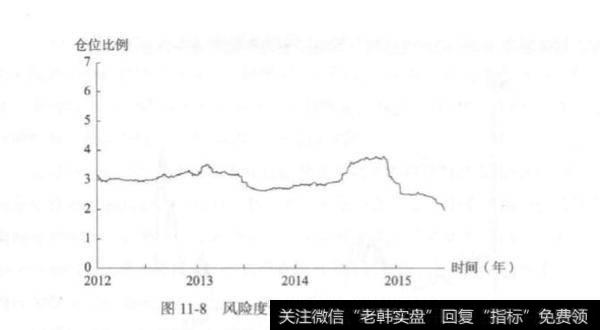
当标准差的阈值取为0.04时,我们基于推进分析中每一行的白色框数据,分别计算出使得收益率序列标准差等于0.04的仓位比例设置f风险,并在图11-8中展示这一长度为845的时间序列。
从图11-8中可以看到,当使用标准差作为风险度量指标,并限定阈值为0.04时,合适的仓位比例在3左右浮动,整个检验期内都没有达到6.6667 的上限。这与0.08标准差阈值下的情况存在区别。
接着,我们把使用凯利公式与风险度量指标得到的仓位比例时间序列放在一张图中加以对比,实际上就是将图11-3和图11-8重叠,如图11-9所示。很明显,使用这两种方法分别得出的仓位设置几乎不再重合。除-天以外,在其余所有时间里,通过限定风险度量指标数值得到的仓位设置都要小于凯利公式计算得到的仓位设置。
那么,当我们使用求取两种仓位决策较小值的方法得到最终结果时,最后使用的仓位设置实际上基本就是基于风险度量指标限制所得到的仓位设置,也就是图11-8所示的曲线。由于图形近乎- _致,这里就不再多做展示,请读者直接参考图11-8。该仓位比例设置,既是推进分析中白色框逐行优化的结果,也是在灰色框中逐日使用的仓位决策。
先分别查看白色框和灰色框内的均线趋势策略收益表现。将整体综合起来进行计算得知,用来优化的白色框内策略平均的年化收益率为132.16%,而用来检验策略的灰色框的年化收益率为10.53%。
可以看到,相较于标准差阈值取为0.08的情况,白色框内的平均年化收益率更小,但灰色框内的年化收益率已由负转正,说明由仓位决策造成的过度拟合程度下降了。这种过度拟合程度的下降,表面上是由改变风险标准导致的,归根到底是缩减仓位所致。
再将灰色框三年半的时间按半年为单位划分为7个部分,考察每半年中的优化期年化收益率和检验期年化收益率情况,结果如表11-2所示。与表11-1对比可知,通过调整标准差的阀值水平,虽然几个原先录得正收益的时期特别是2014年下半年,收益水平有所下降,但是原先收益为负的时期的损失情况均有所好转,2015 年上半年甚至由负转正。

图11-10展示了仓位优化的均线趋势策略在推进分析的框架下,模拟交易过程以1为初始值的净值走势情况。在2012年年底.2013年年底和2014年年底,策略的净值分别变为0.6306. 0.3370 和1.2918。

实际上,在2012~2014年三年间,策略净值水平在大部分时间内都是小于初始净值1的。净值从2014年末开始呈现出一个上升态势,在2015年6月12日达到最高点2.7083,随后的一小段时间有一个较为明显的下跌,到2015年6月30日收盘时的策略净值为1.4194。
基于整个交易过程来看,三年半的策略收益率为41.94%,年化收益率为10.53%,说明该仓位设置下的均线趋势策略存在一定的盈利能力。这是与不进行仓位优化或者将标准差阈值设为0.08时的均线趋势策略的最大区别所在。
前文说过,当标准差阈值设置为0.08时,使用既定仓位决策方法得到的仓位设置过重。这里将标准差阈值设置为0.04,仓位设置随之下降,盈利能力就增加了,是一个实际的例证。
在整个三年半的模拟交易中,策略净值的最大回撤率为78.56%,回撒的发生从2012年1月5日收盘的1.0901开始,一直到2014年4月9日收盘时的0.2338结束,整个回撤过程一共经历543个交易日,与第7章7.1节中的策略最大回撤期完全一致,时间较长。
经过计算,均线趋势策略在整个交易过程中平均的年化最大回撤率为50.53%。对比第7章中不进行仓位决策时策略的年化最大回撒率20.25%,风险有所升高。这是仓位加重所带来的几乎必然的结果。











