对数正态分布下的权证价值与风险规避
在路易斯·巴彻里亚研究的基础上,凯斯·斯普克林 Case m. Sprenkle)进行了进一步的研究,1964年在《认股权价格是预期和偏好的指示器》一文中,凯斯·斯普克林解决了路易斯·巴彻里亚文章中的两个问题。他假设股票价格是对数正态( Logarithmic normal distribution)分布的同时,允许在随机游走中存在漂移项(这就排除了证券价格为负,同时也允许风险规避),其均值和方差均为常数,得出看涨权证的价值由式(3-2)决定:为了更好地理解斯普克林模型思想如何接近布莱克斯科尔斯的思想,下面将斯普克林模型作为布莱克斯科尔斯模型的修正:
3-2
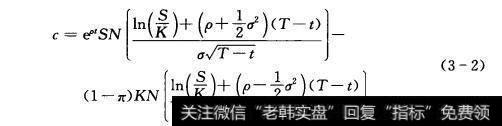
式中:S为股票价格;K为执行价格;T-t为有效期限;参数p为股票价格的平均增长率;π则是风险规避的度量。
凯斯·斯普克林的研究将假设股票价格满足动态的几何布朗运动,而不是算术布朗运动这一论点更接近现实。该成果提高了权证价值判断与风险评估的准确性,为今后的研究提供了有益的尝试,作为现今最为经典的 Black-Scholes模型的创始者—费希尔·布莱克( Fischer black)曾经公开说明,他和马龙·斯科尔斯( Myron Scholes)使用斯普克林的文章得到了他们方程的解。
但是这一判断模式同样没有对股权的期望值进行贴现,并且在实际运用中存在一定的困难,如获得认股权证的价格前首先必须对股票价格的平均增长率ρ和风险厌恶系数x作出估计,但这两者的估计很困难甚至凯斯·斯普克林自己也没有能够估计出p和π的值。











