杠杆PME
杠杆PME(Levered PME)是在基础上,对折现率增加了一个调整系数日。对折现率调整,相当于对折现率增加了一个β杠杆,因此称为杠杆PME。计算公式如式7-12所示。

公式中字母含义与7-4式相同。当β=1时,PME(β)=PME;当β=0时,PME(β)=TVPI。所以,PME与TVPI都是杠杆化PME的特殊值。至于月取值高低,取决于评估者对于风险投资基金风险溢价的判断,风险越高,β取值越大,当然杠杆调整作用越明显。
Robinson & Sensoy 报告了来自美国和欧洲的295家成立于1984-2009年间的风险投资基金的均值、中位数、方差等情况,如表7-4所示。表中已完全清算的基金有192家,剩余为未清算基金。在计算未清算基金PME时,类似于的计算,对于未分配项目做价值评估。相对于标普500指数的PME,纳斯达克指数PME较高一些,2倍杠杆的PME较低一些。
表7-4基础与调整PME
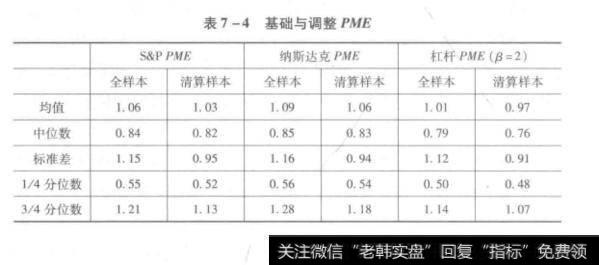
观察表中数据,基金收益均值大于中位数,表现出右偏分布特性,即较少的基金获得了较高的收益率,大部分基金获得了较低的收益率。不论哪个样本,不论使用基础PME还是调整PME,基金收益中位数均小于1,说明大部分基金收益没有赢过指数(包括纳斯达克2000指数和标普500指数)。大部分基金的低收益被少数基金的高收益光环所遮盖了。
GPME
Korteweg & Nagel 提出了一种对PME进行广义调整的方法,称为GPME(Generalized PME),即广义PME,是在PME的基础上,不仅考虑了公开股票市场风险,而且考虑了每个基金的特殊风险,进一步调整PME。计算公式如式7-13所示。

t是第一次现金流发生年度(以年度为时期单位),Qt+h(j)的)是基金在t+h(j))年的退出现金流与投入现金流之比(基金退出收入除以资本投入),h(j)是第j个现金流从t年末开始计算的年数,例如:在第t年年末发生的现金流t+h(j)=t,J是净现金流的总个数。M是基金在时期(t+h(j)),h(j))的随机贴现因子SDF(Stochastic Discount Factor),计算公式如式7-14所示。

式中h是h(j)的简写,r是基于CAPM竹计算的资产组合收益率(收益率加1)的对数,r是市场上小规模成长资产组合超常收益率(超过市场收益率的收益率)的对数(收益率加1的对数),a、b1、b2是参数。
观察公式7-13,Q相当于公式7-12中的D除以PI,而M相当于分子、分母公用一个折现因子。Korteweg & Nagel 的思路就是对折现因子进行调整。尽管Korteweg&Nagel方法未必准确描述风险投资基金收益,但至少提供了一种调整思路,即根据评估者判断,调整7-14式中的a、b1、b2参数取值,或者在式7-14中增加调整项。
Korteweg & Nagel 报告了来自美国的545家在1979—2008年成立的风险投资基金PME和GPME情况,如表7-5所示。第(1)列a=0,b1=1,不考虑b2,GPME=PME=0.048;第(2)列a=0.088,b2=2.650,仍不考虑b2,GPME=-0.103,已经明显低于PME;第(3)列a=0.090,b1=2.680,b2=-0.154,GPME=-0.106。可见,随着考虑的风险因素越来越多,以及参数取值的变化,CPME相对于会发生很大变化。
表7-5GPME的计算与比较












