金融期权价格基础知识:二项式期权走价棋型
二项式模型或二项式期权定价模型(BinomialOptionPricingModel)是由卡克斯(Cox)、罗斯(Ross)和罗宾斯泰因(Rubinstein)于1979年在《金融经济学杂志》发表的文章中提出的。后来卡克斯和罗宾斯坦因(1985年)又对之进行了改进,形成了较完.整的理论范式。
两时期的二项式模型
回顾前面的讨论,1时期股票价格有两种变化的可能:Su和Sd则期权在这一时期价格cu,或者为cd。这些变化成为第2期股票和期权价格的基点。沿着Su方向,股票在第2期也可能上升为Su^2,也可能继续下降为Sud。假设在第2期中股票价格上升与下降的速度仍保持不变,因此我们可以求出股票价格在这一时期各种可能的数值:

在11.6图中,左图反应的是股票价格的变化,右图反映的是期权价格的变化。
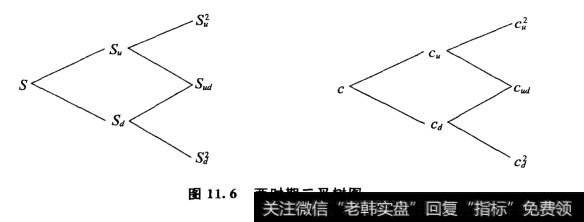
图11.6两时期二叉树图
为了求出0期欧式看涨期权的价格,我们可以把右图分解为三个一时期期权价格的变化过程。
运用前面分析一时期的二叉树图时所得到的有关公式来求和cu、cd和c。

这里的c仍然符合风险中性股价,p^2、2p(1-p)、(1-p)^2仍可解释为cu^2、cud和cd^2出现的概率;e^-2rT代表第2期期末期权价值的折现因子。一期二项式模型中提到的三个步骤仍然适用。
例10,对一时期模型中的例子稍作修改。假定该欧式看涨期权到期时间为6个月,其他条件不变,股票价格每3个月上升或下降20计算cu、cd和c。
根据已知条件,












