金融期权价格基础知识:二项式期权走价棋型
二项式模型或二项式期权定价模型(BinomialOptionPricingModel)是由卡克斯(Cox)、罗斯(Ross)和罗宾斯泰因(Rubinstein)于1979年在《金融经济学杂志》发表的文章中提出的。后来卡克斯和罗宾斯坦因(1985年)又对之进行了改进,形成了较完.整的理论范式。
一、 基本假定
二项式定价模型是建立在以下基本假设基础上的:
1.市场没有摩擦,市场是竞争性的;
2.不存在无风险套利机会;
3.对卖空没有限制;
4.无风险利率为常数,且对所有到期日都相同。
二、 一时期的二项式模型
我们先来讨论一种简单的二项式模型,被称为一时期二项式模型。
假设当前是第0期,欧式看涨期权价格是c。根据基本假设,第1期的股票价格可能上升,也可能下降(假定未来市场只有两种状态,对应两个可能的市场价格)。当第一种状态发生时(价格上升),股票价格由S变为s„;当第二种状态发生时(价格下降),股票价格由S变为Su。这样,第1期的期权价格也有两个取值:上升(Cu和下降(Qd)。
图11.5描述了这两种情形。由于这种图形很像一个叉开的树枝,所以被形象地称为“二叉树”。
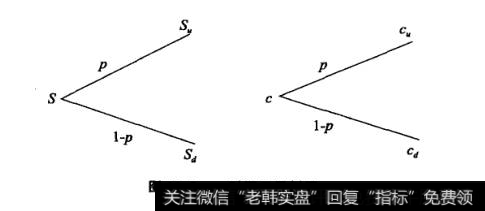
图11.5一时期二叉树图
左图反映了股票价格的运动过程,第0期价格为S,第1期价格为Su或Sd。我们假Su=uS,Sd=dS,其中u≥l,0<d≤l。右图反映了欧式看涨期权价格的运动过程,第0期价格为c,第1期价格为cu或cd。则:
cu=Max(0,uS—X) *
cd=Max(0,uS—X)
我们可以构造一个无风险的证券组合,该证券组合中包括h只股票多头和一只看涨期权空头。股票的现期价为S,期权的现期价格为c,如果用V代
表该证券组合的现期价格,则V=hS-c.
在到期日(即第1期),如果股票价格为uS,则该证券组合的价值变为Vu;如果股票价格为dS,则该证券组合的价值变为Vd使用前面的符号,可以得到:
Vu=hSu—cu=huS—cu
Vd=hSd一Cd=hdS—cd
一个无风险的证券组合意味着,无论在到期日其价值是变成Vu还是Vd,名义收益都是一样。也就是说Vu=Vd,即:

上式表明,需购买的股票数等于一期中期权价值的变动幅度与股票价格的变动幅度之比,或者说,同一期末两节点之间期权价值的差值与股票价格的差值之比。
期初证券组合价值S/i—c,根据无套利原理,应该有:

(11.20)和(11.21)就是一时期的二项式模型。
借助于(11.20)和(11.21),我们就可以计算出只有一期的期权价格。其步骤为:
1.计算p,使证券组合的期望回报率等于无风险利率;
2.计算期权到期时的期望现金流pcu+(1-p)cd;
3.按无风险利率折现上述现金流,折现因子为e^-rT得出期权的理论价格。
例9,一个欧式股票看涨期权,协议价格为26美元,到期时间3个月。标的股票当前市场价格25美元。3月后,股票价格要么上升到30美元,要么下降到20美元。无风险利率年连续复利率10%。计算该欧式看涨期权的价格。根据题意得:

因此,该欧式看涨期权的价格为2.2美元。
对于一时期期权定价公式,需做以下说明:
(1)0期的期权价格是对第1期期权价格的各种可能取值进行加权平均后的贴现值,权重分别是p和(1—p)。但是,回想一下推导过程,我们对股票价格上升没做任何概率假设。因此,可以断定这里的p和(1—p)并不是真实的概率。只不过P在公式中的地位和特征(0<p<1)使其看上去像概率。即如果把p解释为股票价格上升的概率,则(1一P)自然就是股票价格下降的概率。
(2)把解释为股票价格上升的概率相当于假定股票的回报率等于无风险利率。如果所有相关联的金融市场上的投资者都是风险中性的,将没有人要求以更髙的回报率补偿高风险证券的投资。那么,所有的证券包括股票的回报率都将等于无风险利率。因此,也称为风险中性概率。我们将继续在这一风险中性假设下探讨期权定价问题。











