为了下一讲的内容——配对交易,本文先来个预热,讲下平稳性与协整。
平稳性/非平稳性
如果数据的参数不随时间变化,则我们称之为平稳,否则为不平稳,下面来看两个序列A与B。
A序列为符合正态分布的一组数据,均值与方差分别为0和1

A序列

A序列图
注:可以看到A序列一直在0上下波动
再来生成B序列,B序列的均值引入了一个时间变量,

B序列

B序列图
注:可以明显看到序列的向上趋势
危险的非平稳性
正式的论文中,都需要对数据的平稳性做深入可靠的验证,如果你忽略了这点,就可能得到毫无意义的结果。我们在这里使用上述的B序列,先来计算下其均值

计算B的均值

示例图
注:均值体现了所有数据的平均水平,但是对于预测未来状态则是毫无意义的,因为掺杂了不同时间的不同状态,对在不同时间点的统计结果进行比较也是徒劳的。这只是一个简单的例子,用来说明非平稳性对我们的分析造成的影响,在实际中存在更多此类为题,请务必小心。
平稳性检验
一般使用扩展迪基-福勒检验(Augmented Dickey–Fuller test )对平稳性进行检验。

adf检验
注:可以看到结果符合预期,A序列是平稳的,而B序列是不平稳的
移动平均表达法/沃尔德理论
在时间序列分析中,移动平均表达法是一个重要的概念,一个时间序列Y的表达式定义如下:

移动平均表达法
其中η是确定的,比如是正弦波形,因此我们可以很好的对其建模。但是递进过程则是随机的,只能通过时间逐步推导新信息。
其中的递进序列ε的定义如下,其代表t时间点前数据无法解释的随机部分:

递进序列定义
注:bj表示ε对于Yt的影响程度
单整阶数(Order of Integration)
我们将单整阶数为i写为I(i),如果一个时间序列在移动平均表达法中满足以下条件,则称单整阶数为0,既I(0),通常也说,序列的自关联性衰退很快。

I(0)条件
注:对于所有稳定性序列,均满足I(0),但满足I(0)却不能得到其一定为稳定的
有了I(0)的定义,接下来我们就可以通过归纳法逐步构建其他的单整阶数了。
如果一个序列满足I(0),那么对其进行累加操作,新序列就是I(1),再以此类推可以得到I(n)的序列。
下面我们来操作A序列,得到其对应的I(1)及I(2)序列

产生I(1)序列

I(1)序列图示

产生I(2)序列

I(2)序列图示
相反,如果从高阶的序列得到低阶的序列,需要使用差异函数进行处理。

高级转低阶
引入L为滞后算子,最终可以得到低阶序列为:

低阶序列
实例
我们使用微软的股票数据来实践一下以上的内容,首先获取2014年度每日股价数据,

获取价格数据
对其进行平稳性检测,可以看到价格是不平稳的,从图中也可以明显看到

示例代码

价格示例图
接下来我们使用diff函数将价格变化为每日收益,

价格示例图

价格变动图
注:可以看到,神奇的事情发生了,价格的变动序列是平稳的。你可以尝试自己使用pct_change替换diff函数,可以得到每日收益率序列也是平稳的
在量化金融中,常用收益来进行建模,因为它比价格要平稳的多,从而预测也更加稳定,但是在现实操作中也要一定注意,任何收益预测中的谬误可能会在某个时间被放大,从而导致极大的损失。
协整(Cointegration)
假设时间序列Y为时间序列(X1,X2,...,Xk)的线性组合,如下:

线性组合
如果(X1,X2,...,Xk)的单整阶数均为I(1),但它们构造的线性组合的单整阶数为I(0),则称这些序列为协整的。
在量化金融中,对于协整的序列组合应用也非常广泛,最常见的就是配对交易,下一篇文章会进行专门的介绍,配对交易简单说来就是,利用协整的序列组合的噪声会自行回归的特征来进行交易。
依旧使用一个示例来进行说明,X1与X2均为非平稳序列,其中X2为X1加上一个正态噪声数据产生

示例代码
对X2使用diff函数,并检查其平稳性,可以得到X2依旧为I(1)

X2为I(1)
注:对X2进行diff后的序列为平稳的/I(0),说明X2本身为I(1)
再来看看Z=X2-X1组合的情况

协整组合

示例图
协整性检验
有很多种协整性检验的方法,但通常我们都是通过解出一个可以得到I(0)线性组合的系数序列(b1,...,bk),然后对其进行平稳性检验,你可能想到这并不准确,因为可能并没有处理到所有的可能性,确实如此!但是在这里并无大碍,因为不会导致我们做出错误的预测。
在实际操作中,通常会使用线性回归得到相关系数β
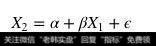
线性回归
然后移除X2对于X1的依赖,剩下的就应该为平稳的噪声数据。

移除依赖
接下来使用真实数据来进行一次协整检验,获取两支股票2014年的股价信息,

示例代码

示例图
注:从图中就可以看到明显的相关性
然后通过最小二乘法回归得到β

最小二乘法得到β
最终构造组合并检查平稳性

构造组合并检查平稳性

示例图
结论:最终该组合通过了平稳性检验,我们即可认为X1与X2的该线性组合是协整的。











