(三)买进看跌期权(BuyPutOption),也称为看跌期权的多头
买进看跌期权,是指期权购买者在支付期权费后,所拥有的可在未来某特定时间,以协定价格向期权出售者卖出一定数量的某种金融商品(或金融期货合约)的权利。投资者之所以买进这种期权,是因为他预期标的资产的市场价格将要下跌。
买进看跌期权后,如果标的资产的市场价格果然下跌,且跌至协定价格之下,则该投资者可行使其权利,以较高的协定价格卖出他所持有的标的资产,从而避免市场价格下跌所造成的损失。如果期权购买者并不持有标的资产,则在标的资产的市场价格下跌时,以较低的市场价格买进标的资产,然后再以较高的协定价格卖出标的资产,从而获利。获利的幅度大小受标的物市场价格下跌的幅度而决定。反之,在买进看跌期权后,如果标的物的市场价格没有下跌,或者反而上涨,则投资者可放弃期权,此时他所损失的是已经支付的期权费。
一般认为,对看跌期权的购买者而言,其潜在的损失是有限的(仅限于他所支付的期权费),而其潜在的盈利却是无限的。但事实上,对看跌期权的购买者而言,即使从纯理论的角度而言,其潜在的利润也不可能是无限的——这是因为任何标的资产的市场价格都不可能跌到零以下。换言之,即使在极端情况下,各种标的资产的市场价格也都以零为其下跌的极限。同时,在购买这种看跌期权时,投资者总得支付一定的期权费,而期权费又不可能为一负值,即使是无内在价值的看跌期权也是如此。于是,对看跌期权的购买者而言,其潜在的最大利润也只能限于协定价格与期权费之差。
例3,某投资者购买了1000股距到期日有6个月IBM股票的欧式看跌期权,协定价格为70美元,每股的期权费为6美元(这样,投资者的初始投资是6000美元)。假定IBM股票的现价为65美元。
如果在到期日股票价格为59美元。投资者可以以每股59美元的价格购买1000股股票,并按看跌期权合约的规定,以每股70美元的价格卖出相同的股票,实现每股11美元的盈利,可以实现11000美元的总盈利(忽略支付的期权费)。如果扣除初始支出成本6000美元,则净盈利为5000美元。
如果在到期日股票的价格高于70美元,看跌期权在到期日时价值为零,投资者每一股的损失为6美元,即总损失为6000美元。表12.3详细解释了该例。图12.3显示了投资者每股股票期权的净损益随到期日股票价格变化的情况。
由图12.3可知,在投资者买进看跌期权的情况下,盈亏平衡价格等于协定价格与期权费之差。如以表示盈亏平衡价格,以X表示协定价格,以P表示看跌期权的期权费,则:BP=X—P
在上例中,盈亏平衡价格BP=70—6=64美元

表12.3看跌期权多头的损益分析表
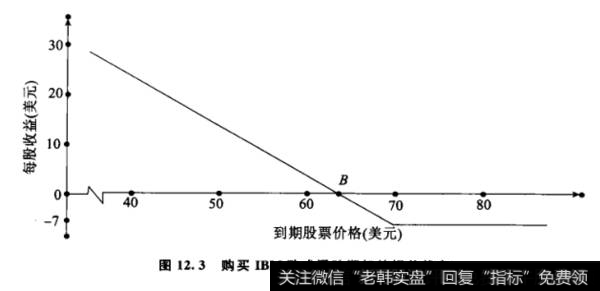
图12.3购买IBM欧式看跌期权的损益状态
(四)卖出看跌期权[SelKWrite)PutOption],也称为看跌期权的空头
对投资者来说,尤其是对套利者与投机者来说,卖出看跌期权的目的是通过期权费的收取来获得收益。投资者能否获得这一收益,即他们收取的期权费能否抵补他们因出售期权而招致的损失还有余,决定于他们对期权标的物的市场价格的预期是否准确。
在一般情况下,若投资者对市场价格看涨,他们就卖出看跌期权;而若投资者对市场价格看跌,则他们就卖出看涨期权。由此可见,期权之“看涨”与“看跌”都是对期权购买者而言的。而对期权出售者而言,则情形正好相反。
从获取利润的角度而言,投资者卖出看跌期权与他们卖出看涨期权一样,其最大利润是他们所收取的期权费。所以,对投资者来说,他们卖出看跌期权的最大利润也是有限的。但从产生亏损的角度而言,则因卖出看跌期权与买进看跌期权在盈亏方面的对称性,投资者的最大损失便是协定价格与期权费之差。
例4,某投资者出售1000股距到期日有6个月IBM股票的欧式看跌期权,协定价格为70美元,每股看跌期权的期权费为6美元(则期权费为6000美元)。假定股票的现价为68美元。
如果在到期日时IBM股票价格低于70美元(假定为59美元)时,看跌期权的多头会执行该期权,看跌期权的购买者可以以每股59美元的价格购买1000股股票,并按看跌期权合约的规定,以每股70美元的价格卖出相同的股票,实现每股11美元的盈利,实现11000美元的总盈利(忽略支付的期权费)。那么,该看跌期权的出售者(看跌期权的空头)就损失11000美元,如果扣除收到的期权费6000美元,净损失为5000美元。
如果在到期日时IBM股票价格高于70美元或更高时,看跌期权的多头认为无利可图,会放弃履约,这时看涨期权的出售者将获利(期权费)6000美元。
表12.4详细解释了该例。图12.4显示了投资者每股股票期权的净损益随到期日股票价格变化的情况。

表12.4看跌期权空头的损益分析表

图12.4出售IBM欧式看跌期权的损益状态
由图12.4可知,在投资者出售看跌期权的情况下,盈亏平衡点价格等于协定价格与期权费之差。如以BP表示盈亏平衡点的价格,以X表示协定价格,以P表示看跌期权的期权费,则:BP=X~P
在上例中,盈亏平衡价格BP=70—6=64美元。











