一般来说,在任何时点,短期和长期利率都是不同的。有时短期利率高一些,有时会低一些。图8-5描绘了两个世纪的短期和长期利率,给我们展现出关于这个问题的一个长期的视角。如图8-5所示,短期利率与长期利率之间的差异由0到几个百分点之间不等,并且有正有负。短期利率与长期利率之间的关系被称为利率期限结构(term structure of interest rates)。更确切地说,利率期限结构告诉我们任一到期期限的无风险、纯折现债券的名义利率。从本质上说,这些利率是纯利率,因为他们不包含违约风险,而且其未来是单笔全额支付的。换句话说,期限结构告诉我们不同时间长度下金钱的纯时间价值。

图8-5 1800-2007年美国利率
当长期利率高于短期利率时,我们说期限结构向上倾斜,而当短期利率更高时,我们就称期限结构向下倾斜。期限结构也可以呈驼峰形状。当出现这种情况时,通常是由于在较长的到期期限内,利率先上升后下降。期限结构最常见的形状,特别是在现在,是向上倾斜的,但陡峭程度的差异相当大。
到底是什么决定了期限结构的形状呢?主要有三个基本的组成部分。前两个是我们在前一个部分所讨论的实际利率和通货膨胀率,实际利率是投资者对于放弃资金使用权所要求的补偿。在调整了通货膨胀的影响之后,你可以将其视做货币的纯时间价值。
实际利率是许多因素的综合函数。比如,我们现在来想一想预期的经济增长。高预期经济增长有可能会使实际利率上升,而低预期增长则有可能使其降低。实际利率可能会因成熟期的不同而不同,这是由于其他因素所导致的经济增长的预期不同所致。比如,对于短期债券来说,实际利率可能较低,而对子长期债券来说则较高,这是因为与长期相比,市场在短期内对经济增长的预期较低。但是,实际利率对于期限结构的形状其实仅有微小影响。
相反,未来的通货膨胀因家则会非常强劲地影响期限结构的形状。投资者们考虑到借出不同期限长短的资金时,他们意识到未来发生的通货膨胀将会侵蚀所回报的货币的价值。因此,投资者们通过要求更高的名义利率的方式对这部分换失求得补偿,而这额外的补偿就被称做通货脚胀溢价((inflation premium)
如果投资者认为通货膨胀率在未来将会更高,长期名义利率将会高于短期利率,那么向上倾斜的期限结构将会反映出在通货膨胀率上的预计增长。同样,向下倾斜的期限结构在很大程度上反映出对于未来通货膨胀率将会下降的预计。
与期限结构有关的第三个组成部分,同时也是最后一个组成部分,就是利率风险。正如我们在本章早先讨论过的。与短期债券相比,长期债券在利率上升时受损失的风险更大。投资者意识到这类风险,因此他们要求得到额外的补偿,这种补偿就通过要求更高的利率来体现。这份额外的补偿被称做利率风险溢价(interest rate risk premium)。距到期日的时间越长,利率风险越大,因此利率风险溢价将会随着到期期限的增加而增加。但是正如我们之前讨论过的,利率风险的增加速率呈现下降的趋势,因此利率风险溢价也将呈现同样的变动趋势。
将所有的部分都放在一起,我们看到期限结构反映出实际利率、通货膨胀溢价以及利率风险溢价三者的综合影响。图8-6展示了这些是如何相互影响以形成向上倾斜的期限结构(图8-6a)或是向下倾斜的期限结构(图8-6b) ,如图8-6a所示,要注意预期通货膨胀率是如何逐步增加的。同时,利率风险溢价上升的速率呈下降趋势,因此其综合而成的效果就必然会是一个向上倾斜的期限结构。如图8-6b所示,通货膨胀率预期在未来会有所下跌,而这种下跌足以抵消利率风险溢价,同时产生向下倾斜的期限结构。注意到如果通货膨胀率的预期下跌仅仅是很小的数值,那么在利率风险溢价的作用下,我们仍有可能得到向上倾斜的期限结构。
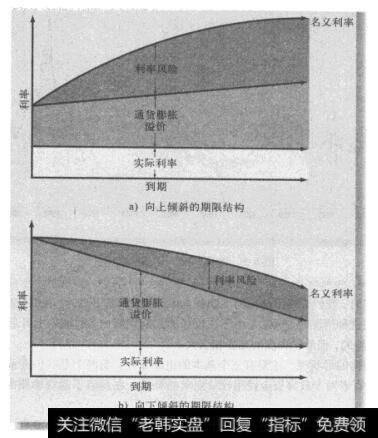
图8-6 利率期限结构
我们在绘制图8-6时假定实际利率将会保持不变。但是正如之前所述的,预期未来的实际利率将会大于或小于当前的实际利率。同时,为了简化起见,我们运用直线来表示预期未来的通货膨胀率的上升或下降,但是他们并不一定得是这样的形状。举例来说,他们可能先上升后下降,从而形成一条双峰曲线。











