期权定价模型有哪些?
期权模型对于期权交易商来说至关重要,每个人都应该掌握某种形式的期权定价模型。在芝加哥期权交易所(CBOE)网站www.cboe.com上有个免费的模型。有一些模型比较奇特而且成本适中,也有一些模型是成熟投资组合管理软件系统的一部分,成本较高。在本书后面就予以详细讨论。
Black- Scholes模型
最著名的期权定价模型是 Black- Scholes模型,由费希尔布莱克( FisherBlack)和迈伦·斯科尔斯( Myron Scholes)教授发明。那时他们和另一位教授罗伯特·默顿( Robert Merton)紧密合作。由于在模型基础上的观点分歧,默顿( Merton)继而独立开展他自己的研究,而布莱克( Black)和斯科尔斯( Scholes)用自己的名字对现在这个有名的模型予以命名。
该模型荣获了1998年的诺贝尔经济学奖。费希尔·布菜克( Fisher Black)那时已经去世,并且诺贝尔奖在他死后没有授予他,但是斯科尔斯( Scholes)和默顿( Merton)分享了该奖。然而,不要认为期权模型可以消除期权定价中的所有猜疑。如果你可以准确描述基础证券价格将会如何运动,这些模型可以给出期权价格的很好的估计。当然,描述基础正确的未来变化是不可能的。这些模型仍然是有用的,可以给出期权成本的估计值,并帮助你判定是否要买入某“标价过高”的期权。
一些使用者发现 Black- Scholes模型存在一些小的问题,所以一些其他模型,如二叉树模型,得到一些人的支持。一般来讲,这些模型不会给出有很大差异的期权价值估值,因此使用哪个模型并没有很大不同—只要你使用某些模型。不借助模型进行期权交易是愚蠢的,相对于最优秀、最精明的交易商来说,这一做法将会使你处于极其不利的地位——该劣势将最终使你损失一大笔钱。
Delta模型
模型的优势在于可以给出假设情况的估值。个最简单的模型是期权的 Delta模型。它是指基础工具变化一个点时期权的变化量。看涨期权的Dlta波动范围是0.00和1.0之间。所以如果基础工具上涨一个点,该看涨期权的价格将上涨半个点,然后该期权的 Delta为0.50。看跌期权的Dela的范围为0.00到-1.00,负号表示看跌期权与基础工具反向移动。价内期权具有相当大的 Delta——反映出他们的波动与基础工其相当接近的事实。另·方面,价外期权具有较小的Dela-—表明要想使价外期权获得较大的价值,基础工具需要大的波动。从某种意义上讲,期权的Dta可以视为期权在到期时成为价内期权的概率。表1.2给出了一些带有评论的实例。
表1.2股票价格:120,1999年4月1号

注意:一个变量的变化会导致其它变量的变化。例如,引申波幅的剧烈上涨会改变期权的 Delta。我们将在本书后面予以详细讨论。
利润图与定价曲线
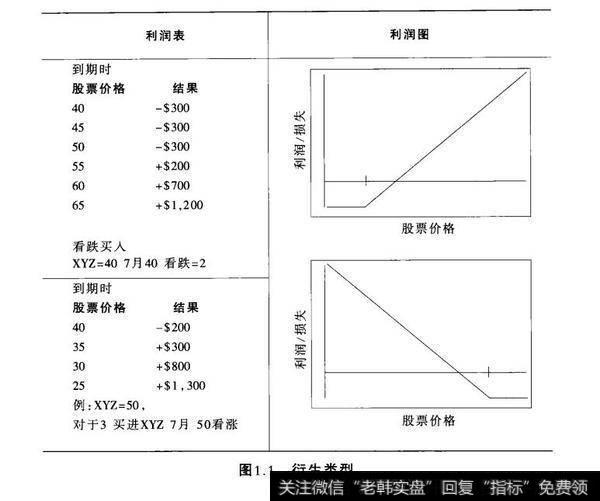
图1.1显示的图形是利润图,描述某一头寸处潜在的利润和损失。这些图形可以通过很多今天在售的期权软件程序以及因特网应用网站绘制出来。当头寸变得比较复杂一一可能涉及众多期权和标的股票头寸—一当基础工具价格发生变化或者随着时间的消逝,利润图可能是唯一能判断头寸变化的方法。多数软件应用程序也使你能够观察引申波幅的变化将如何随着时间的消逝影响你的头寸。
图1.1衍生类型
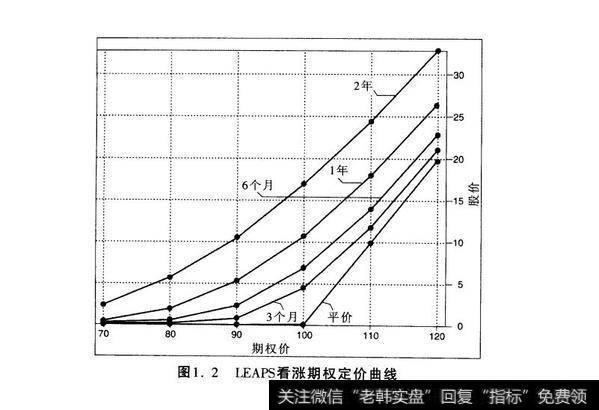
另一方面,价格曲线,是单一期权价值的图形—描述股票价格的一个范围。一个特定的图形可能包含一些价格曲线,通常描述一些简单形式的期权(一样的基础工具,一样的协议价,但是可能具有不同的到期日)。图1.2中的图形就是这种类型的价格曲线。显示了四个期权:3个月期权、年期期权、两年期期权。每个期权都具有同样的协议价100。可以看到这些曲线比较类似,但是期权剩余的时间越长,曲线在图形上就越高。因此,使用这种定价曲线,可以便于观察时间价值以及时间价值的影响。
图1.2 LEAPS看涨期权定价曲线