瑞恩.琼斯在他所著的《交易的游戏》(Wiley,1999)中提出一种非常有趣的资金管理方法。这种方法可以代替固定分数法,这就是固定比例法。
琼斯认为,固定分数法在一定程度上,固然可以加快合约的扩充速度,但会导致某些交易者难以接受的巨大回撤。他的工作就是试图平等地对待每份合约,使资金的增长速率相同。
琼斯对于固定分数法的评价不高。他认为使用这种方法,最初合约的增速很慢,一旦累积到一定数额以后,合约的增速会突然加快。但这需要很长的时间,被琼斯戏称为“10 年”。
他的逻辑是:假设我们拥有00000 欧元,风险比例为10%,最大亏损额为5000欧元,这样最初的风险资金为10000欧元(100000 欧元的10%),可以买进两份合约;当达到150000欧元时才能买进3份合约;因为,150000 欧元的10% 即为15000欧元,所以是3份合约。
下一步就是200000欧元,这时可以买进4份合约(200000欧元的10%为20000欧元,是最大亏损额5000欧元的4倍)。
可以发现,每增加如下数额的资金,可买进的合约就会增加1份:
增加数额=最大亏损额+f%即:增加数额5000:0.1 =50000也就是说,每增加50000欧元就可以多买进1份合约。
瑞恩.琼斯认为(我个人也有同感)。正如我们最初的操作结果,增加50000欧元可以买进2份合约,一旦资金累积到000000欧元,我们就可以买进20份合约。实际上,在第一种情况中,假设每份合约获利2500欧元,只需要10次交易即可(2x2500x10=50000);而第二种情况却只需1次交易(20x2500-50000)。
琼斯指出,最初使用这种方法的成效很慢,一旦资金积累到一定数额,增长速度就会加快,他认为,这可能是可的的回撤所致。对此他提出了自己的解决办法:设定每份合约的增长量相同,或者说,固定每份合约的收益与其增长量之间的比率。如果这个比率为1:5000,这就意味着当每份合约获益5000欧元时,就多买进1份合约,面每份合约的增长量通常被称为“S 值"。
一旦琼斯确定了每份合约的增长量(即“△值"),当每份合约资金的增长量为该数额时,就多买进1份合约。下面我们就用具体实例来解释这一理论。
假设我们最初还是拥有00000欧元,最大亏损额为5000欧元。琼斯并不固定风险比例,而是固定每份合约的增长量(即“▲值"),为了便于理解,我们将这一数值也设定为5000欧元。
一开始系统并没有呈现出规律,所以琼斯只买进了1份合约(还记得在f%中,由于系统的特点和选择的风险,我们最初买进2份合约)。
实际上,只要资金达到105000欧元,就可以买进2份合约;而每分合约的获利额为5000欧元(此种情况下,只能买进1份合约)。
当买进2份合约以后,为了能再增加1份合约(即买进3份合约),每份合约都需要获利5000欧元,即一共获利10000欧元。
因此,只有资金从105000欧元增加到115000欧元的时候,才可以买进第3份合约。而3份合约一共又可以获利15000欧元(每份5000欧元),当资金超过130000欧元时,就可以买进第4份合约;超过150000欧元,也就是获利20000欧元(4份合约,每份均获利5000欧元时,即可以买进第5份合约。
我们从中可以发现差别,最初使用固定比例法只买进1份合约,当资金超过150000欧元时,就可以买进5份合约;而如果使用固定分数法,最初只买进2份合约,当资金超过150000欧元时,也只能买进3份合约。

图4.7描述的是使用两种资金管理方法之后可买进合约数的变化情况。可以发现,在前一阶段中,固定比例法增长得非常快,之后却被固定分数法超越。
很显然,“A 值" (即每份合约的增长量)越低,合约數就增长得越快。因此,交易者就可以通过每份合约的增长量来判断资金管理方法是否得当。
除此以外,琼斯提出最好将“A值"(即每份合约的增长量)设定为系统历史最大回撇数值的一半,但同时也赋予交易者选择风险的自由。
值得注意的是,一旦使用了这种资金管理方法,就不能同时使用其他方法:因为没有给出一个底线(除了缺乏支付保证金的流动资金以外)。如果使用固定分数法,风险比例为10%,一旦资金降到00000欧元以下,就只能买进1份合约,而如果维续下降到5000欧元以下,整个系统都将停止。实际上,5000x0.1-5000 欧元,这也是系统的最大亏损额:如果低于这一数值(也就是说资金总额低于50000欧元),就不可能使用10%的风险比例继续交易。而固定比例法只涉及第一次增长的水平,而不是停止的水平。理论上,只要在保证金允许的范围内,就可以继续操作1份合约。从某个方面来说,这绝对是一个优势;而如果换个角度来说,这也可能导致一些令人失望的结果。
那么,对于固定比例法,可不可以和固定分数法一样,用一个公式来计算买进的合约数呢?
答案是肯定的。此处我们不深究这个公式的推导过程,只介绍它的使用方法:

最初只能买进1份合约,当收益累积到一定数额的时候,就可以买进第2份合约。也就是说,在我们的系统中,资金必须达到52500欧元时,才能买进第2份合约:

的确如此,建议感兴趣的投资者继续验证后续公式。
平均交易即为系统的均线交易。平均说来,每次交易中每份合约的收益即为交易均值。如果用“△值”除以这- -交易均值,即可得到增加1份合约所需的平均交易次数。实际上,在固定比例法中,当每份合约的收益都为“▲值”时,我们就可以多买进1份合约。
在交易过程中,可买进的合约数不断增加,系统的表现也逐渐趋于稳定,不会出现令交易者惊慌失措的巨大波动。
那么,究竟哪种方法更好呢?一般情况下,这主要取决于交易者对股市各种情况的敏感度。在某些情况中,选择哪种方法与最初情况紧密相关。实际上,如果初始资金过少,就不适合使用固定分数法,至少不适合使用较高的风险比例。
下面我们就对固定分数法和固定比例法的合约公式做一个对比。
可以发现,在固定分数法中,合约数与资金额成正比例关系(即等式中的C),而在固定比例法中,合约数又与资金额的平方根直接相关。
这就意味着,在第一种情况中,合约的增加幅度更明显,但初始资金很低的情况除外。除此以外,我们还可以看到,在交易初期使用固定比例法,合约数的增加速度更快,而后期则是固定分数法更快一些。
我们可以从两个截然相反的角度去理解系统的这一表现。
一个思想流派认为固定比例法非常糟糕,因为当资金很少的时候风险很大;而当资金积累到一定数额的时候,风险却又很小。
另一方面,也有人认为固定比例法颇具优势,因为它不仅适用于小额资金交易,而且当资金积累到较高的数额时,还可以有效地保证收益的稳定。
下面再回到我们的欧元/美元系统中,看看分别使用两种资金管理方法,究竟有何不同,它们各自的优势和劣势又是什么。

图4.8中是使用固定分数法时资金的变化情况,风险比例为5%,初始资金为50000欧元(为了方便起见,我们以后都使用欧元而非美元为单位,尽管美元是世界上第一大流通货币。但是,不管使用哪种货币交易,结果都是一样的)。
或许5%的风险比例对大部分交易者来说不算高,如果总资金为50000欧元,风险资金即为2500欧元,相信这对于绝大多数交易者来说都是可以接受的。事实上,让交易者产生心理变化的不仅仅是某一次交易的亏损,而是一连串交易的连续亏损。在图4.8中,资金前半段的走势趋于平缓,而后半段也如使用了凯利公式的曲线图一样,出现了大幅度的涨跌。
但最终结果(654917.5欧元)还是相当令人满意的,与此同时,系统的最大回撤却让人难以接受,超过了350000欧元,即从639920欧元下降到275317.5欧元,跌落了一半还多!

图4.9描述的是一次交易的变化情况,初始资金仍为50000欧元,每次交易的风险比例为10%。
与历史最高值相比,最终结果似乎并不能令人满意。第一个超高峰值就让我们难以置信,而让我们更加难以置信的是紧随其后的回撤,从3173825欧元下跌到476732.5欧元,几乎下降了9成,相信这对于大多数交易者来说,都是一种巨大的打击。
随后我们再次从一堆金蛋中发现了一只能孵出母鸡的蛋。如果将风险比例从10%提高到11%又会出现什么情况呢?下面我们来看看图4.10。

这里发生的情形似曾相识(在凯利公式中同样出现过):剩余资金在理论上是可以继续操作的,而实际上交易却停止了。
利用固定分数法,可推算出最大亏损额为1250欧元,由此可计算可买进的合约数。而当资金变为11235欧元时,计算结果如下:
这时,某些人可能会感到困惑,如果将风险比例设定为11%,风险资金仅为1235.85欧元,系统就停止运行,那么10%风险比例又是如何运行的呢?答案非常简单:从一开始,我们的风险比例就为10%,到达系统的某一点时,剩余的资金就更多;特别是将风险比例设定为11%时,资金减少为11235欧元,这是第129次交易。在同一个交易中,10%的风险比例剩余的资金仍为13547.5欧元,即可得到以下结果:一些小变化可能导致最终结果相差甚远。
值得注意的是,该系统的最优f值约为23.4%。很显然,在这种情况下,不能对该系统使用这一比例,因为这是纯理论数值。唯一的差别就是其跌落后的资金4752.50欧元(见图4.11,为最优f值的尝试),比风险比例为11%时的资金还要少。
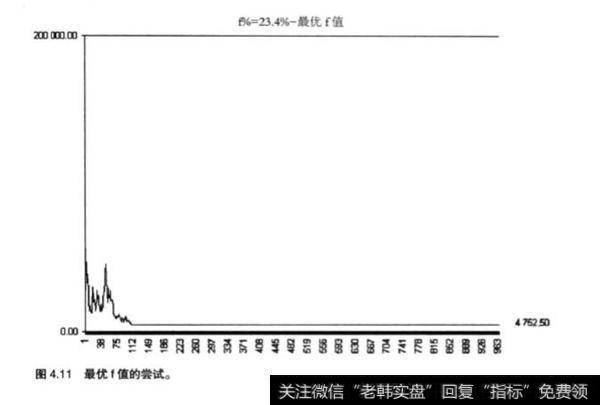
众多周知,如果风险比例太高,就很容易破产;而如果太低的话,就会阻止系统交易甚至根本无法开始。
可用资金为50000欧元,可能的最大亏损额为1250欧元,只有当资金大于1250欧元时,才可以启动交易系统。1250欧元是0000欧元的2.5%,这一比例同时也是该系统可能出现的最小比例,至少在最初是如此。实际上,在第二次交易之后,资金总额就少于50000欧元,交易也就停止了。
接着尝试可以发现,能够保持系统一直交易的最小比例为3.75%,图4.12中描述的就是这一情况,即不致使系统停止的最小风险比例。显然,这一比例是由初始资金决定的,正如使用凯利公式的情况一样。

可以看出,即便使用最低风险比例,回撤也是相当严重的。我们还记得,原始报告(图3.2)并不认为这一系统很好,我们之所以运用在例子中,主要是为了体现使用资金管理方法的效果。
现在我们再来看一下使用固定比例法得到的结果:

这种情况下,是△值决定了合约数的扩充速度。即A值越小,合约的增加速度就越快。
正如第一个测试,我们选取的O值大约是系统历史最大回撤的50%。还记得图;3.2中的回撤大约为22000欧元,因此,我们选取的A值为11000欧元,这就意味着当每份合约的收益为11000欧元时,我们就可以多买进1份合约。
图4.13即O值为11000欧元,使用固定比例得到的结果。

看似没有任何不妥,此外,还能发现其与最小风险的固定分数法曲线有诸多的相似之处。
鉴于以上0值比较高(11000欧元),我们再来看看如果将△值设定为5000欧元和2500欧元时,会得到什么结果。第一种还勉强可以接受,而第二种就相当冒险了(这两个数值的选择并非偶然:它们分别是理论最大亏损额的4倍和2倍)。

可以发现,图4.15中的结果比图4.8(使用固定分数法,f=5%)要好。而实际上,两种情况的回撤幅度都不小。说实话,如果对该系统使用固定比例法,回撤同样很大。但如果要说固定比例法相较于固定分数法的优势,或许就在于前者不存在操作的最低风险极值;而对于固定分数法而言,其风险比例下降到一定程度之后,系统就停止交易了。这也正是固定比例法的优势所在。
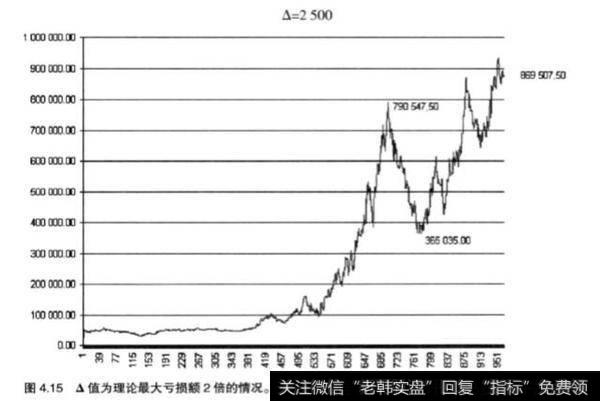
与此类似,使用固定比例法时,也可以超过风险比例的上限,只要在保证金允许的范围内操作即可。
将0值设定为理论最大亏损额(即1250欧元)是非常冒险的。如图4.16所示,可以发现一些很有意思的结果,这种情况下的回撤率与前一种情况类似,都不像图4.9中的情况,令人如此难以接受(与其他风险比例相比)。
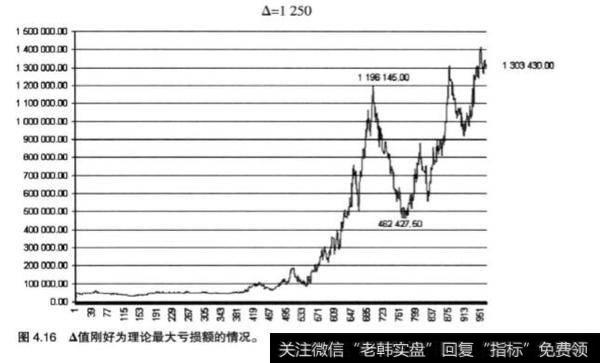
最后,我们假设一种极限情况,如果风险过大,系统就偏离正常的运行规律,如图4.17所示。
可以发现,在这种情况下,资金是无法真正大幅度上涨的,除了系统的黄金时期,此时的峰值增长到4倍还多(224637.50 欧元),但过高的风险随即使资金持续下跌,甚至低于初始资金,直至系统停止交易。
值得注意的是,即便在这种情况下,也并不能排除未来股市利好的可能性,而如果使用的是固定分数法,系统就永久地停止交易了。











