未来业绩控制图表
对过去业绩数据的分析可以帮助区别能够进行相互竞争的RGP和资金经理人,但对未来业绩给出的信息太少。我们发现,很难准确预测未来,但是可以对未来交易结果的范围做一些预测。这种预测属于区间预测,而非点预测,可以帮助我们设计交易或投资策略。
我们借助统计学的中心极限定理(CLT )来实现预测目标。该定理适用于从有限均值μ和标准偏差σ的无限总体中抽取的简单随机样本。CLT理论是,如果样本规模足够大,那么样本均值就符合均值为μ、标准偏差为oh的正态分布。盈利产生过程(RGP)的盈利分布可能是非正态的,但是盈利肯定具有有限的均值和方差,分别为μ和σ。在这种情况下,假设总体是无限的,当n足够大(比如说n>25)时,样本均值统计量接近于均值为μ,标准扁差为σVM正态分布。这就意味着我们在计算出滚动12个月、24个 月或36个月平均盈利后,可以使用正态分布的特性,预测未来12个月的平均盈利范围。例如,我们可以计算滚动24个月平均月盈利以及它们的标准偏差。然后我们可以说,在接下来的12个月里,滚动24个月平均盈利有68%的机会将位于一个在当年年底计算的区间μ土σ 124之内。
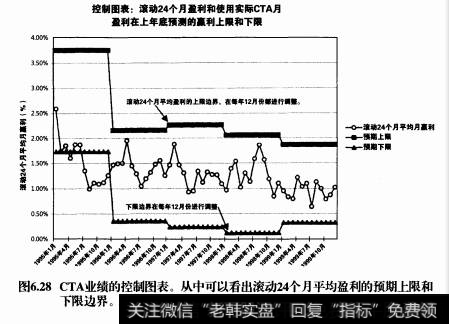
图6.28所示为使用实际CTA业绩数据得出的滚动24个月盈利。图中还画出了使用式子μ2o土o 2/J24得出的滚动24个月盈利的上限和下限,其中μ.:为截止上年12月底24个月的平均盈利,σ:是到截止上年12月底为止的那些滚动盈利的标准偏差。于是,对于1999年使用的预测值便是在1998年底计算的那些。例如,1998年底计算的前24个月平均月盈利为1.10%,标准偏差为3.77%,计算出8历年度1999年的月盈利上限和F限分别为1.87%和0.33%。这意味着什么呢?如果1999年12月底的滚动24个月平均盈利恰好为1.10%,那么上24个月周期上的盈利可以通过合成平均盈利来近似: 100( (1+011**-1)=30% (近似)。999年12月底预期24个月盈利的上限为100( (1+0.187)2*-1) =56% (近似)。类似地,到1999年底为止的两年期预测下限为8.2% (近似)。如同计算结果所示,实际1999年12月平均24个月盈利为1.02%,预测两年盈利为27.5%,实际24个月盈利为26.5%。预测误差产生的部分原因是我们合成的是算术平均盈利而非几何平均盈利。尽管如此,预测中的误差也是可以接受的,因为它给出了一种记录预期盈利和实际盈利的图形方法。
如图6.28所示,当业绩在新的一年里不断变化时,可以使用带有为未来业绩精心设计的上下限的控制图表来记录业绩。比如在1995年,那位CTA的盈利跌破了μ土σJ24带,对此事件我们得到很多警示。在1996年,预测带下移,以适应新的现实,而后业绩又重新强力向预期业绩的上限弹起。从1997年 到1999年之间,业绩限制带没有大的移动,业绩基本位于年底预期范围的中部。所以,我们可以使用历史业绩数据来设计控制图表,为在24个月或36个月周期上平滑后的未来业绩做一个区间预测。也可以使用12个月的平滑周期,但是预测带必须被设得稍宽一些, 以容纳较短时间框架内较大的波动性。











