权证模型使用说明
关于权证价值判断模型,本书的第3章进行了详尽的阐述,不同的理论阶段的权证价值判断模型都有着各自的特点。早期的理论所涉及的模型有:路易斯 巴彻里亚( Louis bachielie,1900年)的标的资产价格与收益具有算术布朗( Arithmetic Brown)运动特性的权证价值判断模型(以下称为A-B模型);凯斯斯普克林( Case M. Sprenkle)的对数正态分布( Logarithmic NormalDistribution)下的权证价值判断与风险规避模型(以下称为LND模型);詹姆斯·伯恩斯( James Boness1964)的时间价值观念( Time Concept)下的权证价值判断与风险溢价模型(以下称为TC模型);保罗·萨缪尔森( Polo A. samuelson1965)的几何布朗运动 Geometric brown)下的权证价值判断与风险差异模型(以下称为GB模型);瑞普和卡斯夫( Thorp&. Kassouf,1967)的投资组合( Investment Portfolio)下的权证价值与风险收益模型(以下称为IP模型)。上述模型除了GB模型相关参数能够在现实中获得,其他模型的参数均无法完整地在市场中获得,在传统理论框架下参与权证价值判断模型有效性的实际检验存在一定的局限性,因此仅将GB模型作为参与比较检验的模型。
经典理论框架下的权证价值判断模型,是1973年布莱克和斯科尔斯建立的BS模型,该模型主要给出了金融衍生品价格与收益在服从对数正态分布的假设下运用无套利原则推导出权证价值判断公式。尽管该模型具有严格的假定,但解决了困扰经济学家大半个世纪的难题即模型中所有涉及的参数均可以在实际操作中得到,所以经典的BS模型是可以作为比较检验的模型权证现代理论是对传统与经典权证价值判断模型的拓展推广和修正。数值理论模型在这一阶段尤为突出,其将BS模型思想运用数值研究方法进行了诠释,如二项式模型( Lattice Approach)、有限差分模型( Trinomial lattice)蒙特卡罗模拟模型( Monte carlo simulations)等。
自20世纪80年代以来,具有数值与分析类综合特征的权证理论也不断得到发展,如具有稀释效应修正的BS模型(以下称为DBS模型)。该模型考虑到在增发标的资产的前提下,对标的资产及其衍生品市场价格的稀释效应,并以此推断出无偿和有偿派发权证价值判断模型(以下称为DBS1,DBS2模型),修正了BS模型的无红利条件,因此,从这一点来说,该模型更具有实际意义。由于无偿派发红利现在已经成为一种常态,所以应采用无偿派发红利修正模型作为参与比较检验的模型。
波动理论抓住标的资产价格波动率是金融衍生品价值判断的关键变量这问题,为权证价值判断提供了更现实的条件。波动率权证理论的发展,解决了权证价值判断的关键变量难以确定的问题,并逐渐成为一个新的趋势。其中以SVGARCH模型, EGARCH模型(以下称为EG),GJR模型和随机波动率(HW)模型最具有代表性。
将上述权证价值判断模型与波动率模型进行汇总如表5-1所示。
表5-1不同理论阶段权证价值判断模型与波动事模型
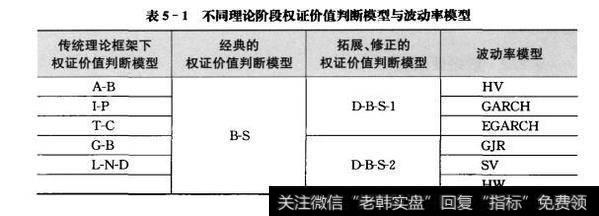
如果将上述价值判断模型中可以实际操作的模型统一在平抑资产价格与收益波动率分析框架下,可以演绎出以下权证价值判断模型,如表5-2所示。
表5-2不同理论框架下权证价值判断演绎模型

由于参与比较检验的模型比较多,为反映模型价格与实际价格的接近程度,定义平均绝对百分比误差来表示各模型价值判断的误差。平均绝对百分比误差:
(5-1)

式中: market-price, model-price分别表示权证的模型价格和市场价格,n表示样本数量。











