为更好地理解负自相关效应,我们可以考虑一个组合,这个组合的回报率在给定的时段可能以20%的幅度增长,也可能以10%的幅度下降(见图10.4)。由于这两种情况是同等可能的,因此单一时段预期回报率的平均值为5%。如果回报率是独立且等概率分布的,在两个时段之后:
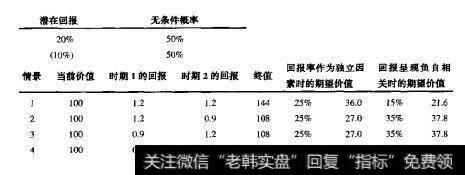
图10.4当回报呈现负自相关时的期望价值
1.初始100美元的投资增长到144美元的概率是25%;
2.初始100美元的投资增长到108美元的概率是50%(包括了两种概率相同的情况);
3.初始100美元的投资减少到81美元的概率是25%。
两个时段的预期价值是110.3美元。如果100美元按照预期回报率的算术平均值5%来算,两个阶段之后的价值也是110.3美元,与前面的计算结果一致(这里都考虑了保留一位小数)。但是如果图10.4中四种情况的可能性不同,两时段的期望价值就不等于110.3美元了。比方说,如果低回报率后为高回报率的概率是70%(反之亦然),那么两时段后的预期价值只有109.4美元。在这种情况下,以算术平均值进行复合就会导致预期回报率偏高。











