上一节所阐述的凯利公式正是量化择时策略进行仓位决策的一种行之有效的方法。在通过上一节内容所形成的基本认识的基础上,我们在这一节中进一步说明实际研发中的仓位决策是如何做出的。
图10-4通过灰色区域说明了仓位决策在量化择时策略研发流程中的位置。可以看到,仓位图的设定既依赖于买卖决策,如第4章、第7章涉 夏机理置及的择时策略中的决策行为,也依赖于量化交易策略对风险的控制。
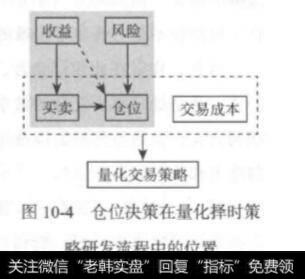
需要注意的是,在凯利公式的设计中,控制的风险是一次性损失掉所有资金的可能性,这是一个相对而言程度比较弱的风险控制行为。对该公式面言,仓位优化更重要的目标在于最大化交易策略的整体收益。图10-4灰色区域中由收益到仓位的虚线箭头,其含义就在于此。
因此,在凯利公式的逻辑下,风险控制对仓位的影响是偏小的。更重要的是,由于凯利公式控制的风险是一次性损失 掉所有资金的可能性,因此当实际的风险大于预估的风险时,凯利公式得到的仓位设置可能就会导致资金一次性损失掉的情况出现。而由于量化交易策略的研究当中不可避免地存在过度拟合的情况,因此回溯测试下策略所表现出的风险往往都小于策略在未来所具有的风险。在这种情况下,凯利公式的风险控制能力是值得怀疑的,单纯地使用凯利公式本身就具有很高的风险。
在实际的量化交易策略研发过程中,虽然凯利公式具有很好的内在逻辑,但是其带来的“安全感”过低,所以我们很难仅仅使用凯利公式来确定策略的最优仓位。解决这一问题最为直接的途径就是提高风险控制的程度,使其不仅仅满足于规避一次性损失所有资金的风险。具体的做法是直接使用风险度量指标来描述风险水平,通过调整仓位设置,保证量化交易策略的风险不超过某一具体水平。
关于风险度量指标,本书已经在第9章的9.1节和9.2节中进行了一定的介绍,这里不再赘述。对一个完整的量化交易策略而言,在买卖设置相同的前提下,设定不同的仓位决策,就会具有不同的风险水平,具体表现为不同的风险度量指标结果。那么要做的,就是确定合适的仓位设置,使得风险度量指标的结果等于研究者事前设定的数值。
当然,在使用风险度量指标确定仓位决策时,一样存在着回溯测试下策略所表现出的风险小于策略在未来真实具有的风险的问题。因此,使用某个风险度量值作为阈值求出的仓位决策,往往也会导致超过该國值的实际风险。在实际中可以通过调低风险度量指标的同值取值来平衡。
在图10-4的研发框架中,不论是使用凯利公式,还是使用纯粹的风险度量指标来确定仓位决策,都是建立在买卖决策已经建立的前提下的。我们知道,最优的买卖决策是基于收益最大化导出的。因此,即使是使用纯粹的风险度量指标来进行仓位决策,整体而言也同时考虑了收益与风险。
而凯利公式与风险度量指标的差异点在于,凯利公式导出的仓位决策更看重收益,风险度量指标导出的仓位决策更看重风险。两者的侧重点不同,是一组比较互补的仓位决策方式。在实际工作中可以同时考虑这两种方式,综合两个仓位决策结果来决定最后使用的仓位决策,如图10-5所示。
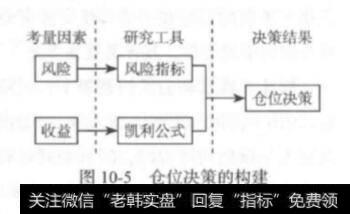
只是在实际的量化交易策略研发中,使用凯利公式所得到的最佳仓位往往都相对较重,通过风险度量指标限制所导出的仓位往往会偏小一些。只要量化交易策略的使用者不是太过激进,一般都会更多地考虑较小的仓位,或至少给予小仓位更多的考量权重。
当然, 凯利公式与风险度量指标这两种方法得到的仓位决策孰大孰小并不是绝对的。鉴于两种仓位决策手段都不难实现,稳妥的办法是计算两个标准下的仓位决策结果,综合进行考虑。比较简单的做法就是取更小的那个仓位设置。

式中,fa是使用凯利公式得到的仓位设置; f风险是使用风险度量指标限定得到的仓位设置。fm利和fr都代表整体资金量的一定比例,因此仓位设置结果J也是一个比例。
上文提到了,不管是凯利公式还是风险度量指标,这两种方法都存在实际风险大于预估风险的问题。表现在现实中,就是回溯测试下策略所表现出的风险,往往都低于策略实际的内在风险,也就低于策略在未来实际表现出的风险,因此将其作为仓位决策的标准时,得到的仓位往往都是过高的。
解决的办法,一是如同前面说的,通过调低风险度量指标的阈值取值来得到一个相对更低的仓位结果,也就是主动调低回溯测试下的风险承受能力;二是干脆直接將仓位设置结果f按比例减小。一般而言,第二种方法虽然直接,而且对凯利公式和风险度量指标两种方法同时有效,但是经过一个中间步骤之后,其内在逻辑性减弱了。当然,第一种方法中如何调低风险水平也是一个缺乏定量方案的问题,研究人员如何选择还需要自行摸索。











