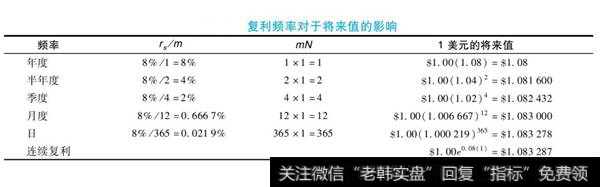
因为报价年利率并不直接给出将来值,所以我们需要一个反映其有效年利率(EAR)的公式。对于按半年度复利计息的8%的年利率,我们将在计息期间(每半年)中以4%的利率计息。在1年的期间中,1美元的投资将增长到$1(1.04)2=$1.0816,如下图所示。
图一
该1美元的投资所获得的利息为0.0816美元,它代表了8.16%的有效年利率。有效年利率可以按如下公式计算:

图二
期间利率是报价年利率除以m,其中m为1年中复利期间数。
利用图一,我们可以求得有效年利率为:(1.04)2-1=8.16%
有效年利率的概念可以用到连续复利上。假设我们有一个8%的连续复利利率。我们可以用与上面相同的方式寻找适当的将来值因子,来求得其有效年利率。在这个例子中,一个1美元的投资将会增长到$1e0.08(1)=$1.0833。在这一年中所获得的利息代表有效年利率8.33%,它要比半年度复利计息的有效年利率8.16%大,因为利息的复利更加频繁了。在连续复利的情况下,我们可以求解得到如下有效年利率:

图三
我们可以逆向使用离散复利和连续复利的有效年利率公式,来得到与给定有效年利率相对应的期间利率。假设我们想要知道给定半年度复利计息的8.16%的有效年利率所对应的确切的期间利率是多少,那么我们可以利用式( 图二)来对期间利率进行求解:

要计算与有效年利率8.33%相对应的连续复利利率(以连续复利计息的报价年利率),我们可以去寻找满足式(图三)的利率:

要解这个方程,我们可以在两边同时取自然对数(回忆一下,ers的自然对数是1ners=rs)。因此,ln1.0833=rs,最终求得rs=8%。于是,我们了解到以连续复利计息的8%的报价年利率与8.33%的有效年利率是等价的。











