规则二:交易规则数量要尽量少
本书所讲的决定性交易系统只使用较少数量的规则和变量。这些交易系统类似人们为控制化学处理过程而开发的任务系统。经验告诉我们,完善可靠的控制系统要使用尽可能少的变量。
下面我们来分析两个著名的趋势跟随系统。最常见的双移动平均线系统只有两条规则。一条是在向上穿越时买进,另一条是在向下穿越时卖出。类似的,流行的20棒线突破系统最少时只有四条规则,即两条入场规则、两条出场规则。如果使用测试软件在多年的历史数据上测试这些系统,可以证明它们是具有盈利性的。
与可能具有数百个变量的基于专家系统的交易系统相比,这些系统怎样呢?例如,某套可以买到的交易系统,其规则数超过400,但实际用于交易的规则只有一条。决定性系统不同于基于神经网络的系统,神经网络系统往往具有未知数量的规则。
试验设计的统计学原理告诉我们]即便是非常复杂的过程也可以用5~7个“重要”变量来控制。极少有系统超过10个主要变量,而且控制超过20个变量的过程是相当困难的。同样,也极少有过程是基于4个或更多变量之间的相互作用。较高次数的相互作用通常是意义不大的。我们的目标是使规则的总数量尽量少。
在设计系统时使用较大数量的变量存在很多隐患。第一,变量规则相对重要性随着规则数目的增加而降低。第二,自由度随着变量和规则数目的增加而降低。当规则和变量的数目增加时,需要更多的数据来测试,以使得到准确的结果。第三, 是在做曲线拟合测试时,所选样本数据带来的风险。例如,给定一组数据,一个带有两个变量的线性回归便足以拟合该数据。当回归分析中的变量数目增加时,比如说7个,那么所得曲线与所给数据更加接近了。所以在做曲线拟合时,我们在所给数据中捕捉了更多的细微变化,这些价格模型在未来可能永远都不会重复出现。对于简单的线性回归,自由度下降了2,但对于多项式回归,自由度却下降了7。
模型都应该尽可能地简单。在这种情况下,简单的线性回归,具有斜坡和交叉,抓住了数据中所有重要的信息。其次,添加复杂的高次项(规则)的确增加了曲线对数据的拟合度。于是,当我们建立更加复杂的模型时,我们在数据当中捕捉到了更多的细微信息。这些细微信息在将来会重复出现的可能性非常之小。再者,我们建立模型的目的是描述价格在测试区间上是如何变化的。使用我们的数据来直接计算线性回归系数,那么,我们的模型是源自所给数据。没有理由表明这些系数会准确地描述任何未来的数据,这就意味着任何过度拟合的交易系统都不可能在将来表现良好。
另一个例子,是移动平均交易系统的一个改进版本,解释了为什么要限制规则的数量。通常情况下,双移动平均系统只有两条基本规则。例如;对于做多入场,3日均线应该向上穿越65日均线,反之亦然。
现在,我们来看一个使用多于两条平均线的变化版本。例如,如果3日均线和4日均线都在65日均线之上时在收盘价买进。既然有两条“短期的”均线,这使我们有了四条规则,两条用于做多、两条用于做空。使用越来越多的“短期”均线可以使得规则的数目快速增加。例如,如果3日、4日、5日、6日和7日均线都应该在65日均线之上时才做多入场,那么就增加了10条规则。
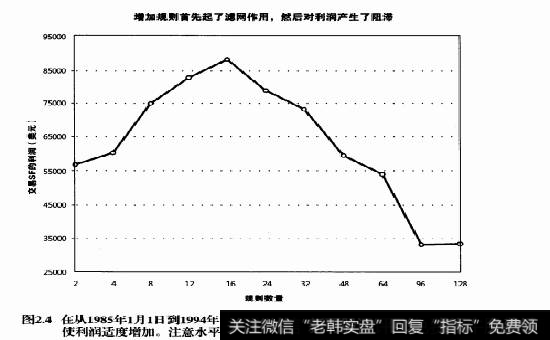
我们来看一下瑞士法郎10年连续合约数据,从1985年1月1日到1994年12月31日,没有任何初始止损,但考虑了100美元的滑移价差和佣金。规则的数目从2条到128条不等,以便研究规则数目的增加对系统的影响。随着规则数目的增加,交易数目减少。 这意味着当增加规则的数目时,我们需要史多的数据来做可靠性测试。
图2.4显示了当我们增加更多的规则时,刚开始的盈利是增加的。这意味着额外的规则首先起到了滤网的作用,减少了许多不成功的交易。然而当我们添加更多的规则时,它们对盈利产生了阻滞作用,大大增加了资金曲线的不平滑性。于是我们应该注意不要增加数十个规则。
如前所述,这个例子没有包含初始止损。所以当我们增加规则的数目时,系统的最大日内回撤应该增加,因为入场和出场都被延迟。
对于美国债券市场从1975年1月1日到1995年6月30日的计算表,上述结果仍然成立。具体的形态将取决下测试数据。其他市场的数据进一步确认增加规则会减少盈利。
因此,增加规则不会产生无休止的益处。因为那样不但需要更多的数据,而且还增加了系统的复杂性,使得系统的性能变差。一个具有许多规则的复杂系统在测试数据当中抓取了大量的细微信息,但是这些价格模型在将米重复出现的可能性几乎为0。所以相对简单的系统在将来更容易表现良好。











