在本文开始前,大家应该清楚一点,样本均值与总体均值是不同的。一般情况下,我们都希望得到总体均值,但是往往只能计算出样本均值,进而使用样本均值去估计总体均值,这就引入了置信区间的概念,置信区间是用来衡量使用样本均值估计总体均值的精确程度。
置信区间
如果想要评估美国女性的平均身高,你会怎么做?你可以能随机测量10名女性的身高,以此来估计整体的平均身高,下面我们使用代码来模拟下这个过程:

计算样本平均身高
很轻松我们就可以计算出样本的平均身高,但是它对于我们却没有太大用处,因为我们无法确定它与总体平均间的关系。
可以通过计算方差来尝试得到样本的离散度,方差越高,则不稳定性与不确定性越高。
计算标准差
但这依旧是不够的,这就需要我们计算标准误,标准误是用来衡量样本均值的方差。
注:在计算标准误之前,你首先需要确保你的样本具有无偏性,并且数据是服从正态分布且独立的。如果没有满足这些条件,那么所计算出得标准误就没法使用,但对于这种情况,也有许多检验与矫正的方式,下文中会提到。
标准误计算公式
由此公式,写出对应的Python代码:

标准误计算示例代码
继续我们的旅程,假设我们的数据是服从正态分布的,那么我们可以使用标准误来计算置信区间。首先,设定期望的置信区间,比如95%,然后就可以确定在多大的偏差范围内可以包含95%的数据,对于标准正态分布来说,是介于-1.96与1.96之间。当样本足够大时(通常>30即可认为足够大),根据中心极限法则,可以认定分布服从正态分布;如果样本不够大时,使用指定自由度的t分布则更为安全。
注意:在使用中心极限法则时要十分小心,因为许多金融数据都是非正态的
下面使用matplotlib绘制一下标准正态分布的95%的置信区间:

绘制置信区间示例代码
绘制图形如下:

95%置信区间
到这里,我们除了孤零零的样本均值之外,还计算出了置信区间,总体均值更有可能落在此区间内。假设我们的样本均值为μ,那么置信区间则为:

置信区间
必读
在任何给定数据的情况下,估计的真值与置信区间都是固定的。但需要注意的是,“美国女性平均身高在63英尺与65英尺之间的概率为95%”这种常见的理解是不对的,正确的解读应该为,“在多次试验中,有95%的试验中,真值会落在计算出得置信区间内”。所以当仅存在一个样本,并计算出了置信区间的情况下,我们是没法评估区间包含总体均值的概率的,下面会通过绘图方式演示给大家。
例子中有100个样本,对于每个样本分别计算其样本均值与置信区间
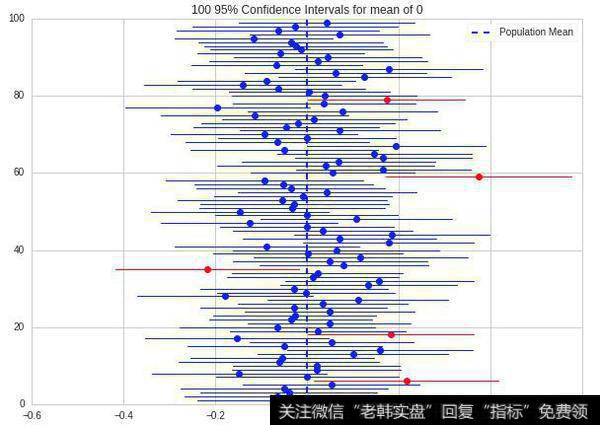
结果图
进一小步
回到本文最初的身高案例,因为样本很小,所以我们使用t检验。使用之前提到的标准误公式,可算出该样本的置信区间

身高案例置信区间
用scipy.stats的内建函数,可以更为便捷地完成计算,但这里需要注意参数中需要传入自由度。

scipy内置函数计算
注:可以看到,伴随着置信水平的提高,置信区间范围也更广
如果假设总体服从正态分布,也可以使用更为简化的方法进行计算,这里就不再需要传入自由度
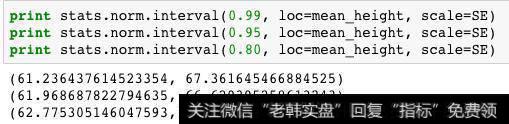
正态假设下计算
现在再来回顾一下,我们设定了一个期望的置信水平,并由此得到了可能包含真值的一个区间,要求的置信水平越高,则区间范围越大。通常情况下都不会使用一个点进行估计,因为其为真值的概率实在太小。值得注意的是,伴随着样本数量的增加,我们得到的置信区间范围会更加精确(小)。
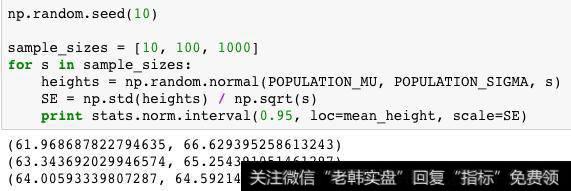
样本数量增加时置信区间缩小
示例
接下来,我们使用一个包含100个数据的样本(正态分布),同时绘制频度柱状图及其均值的置信区间。

100个样本图例

示例图
标准差、标准误与置信区间的计算均依赖于特定的假设,如果这些假设不满足,那么就很有可能导致在你期望的95%的置信水平下,最终得到置信区间达不到你的期望,这就被称作估计错误。
下面就举一个例子,也是非常常见的一种情况——自相关。自相关会导致更多极值,这是因为新值会依赖于之前的值,则已经偏离均值的数据序列则更有可能继续偏离,下面以如下形式的自相关数据来解释一下:
自相关
下面我们产生一个自相关的数据序列,并将其绘制出来

产生自相关数据代码

示例图形











