激进型比例法
显然,也可以反过来对固定比例法使用相同的原理,在资金积累到一定程度之后,增加风险的比例。我们的8的是试图控制回撒幅度,使资金保持持续增长,而我们采用“随着资金的增长减小0值的做法”却恰恰与此背道而驰。
以此为例,可以看出使用固定比例法的变化情况,在这种情况下我们称之为“激进型比例",即每当资金的增长量与初始资金相同时,就将A值降低到原来的90%。并且我们将A值的114 设定为最低值。数值都是任意选取的,它们的唯一目的就是体现所得曲线的变化趋势。
表5.3是△值的变化情况,在这种情况中,初始资金为50000欧元,最初的0值为5000欧元。

从图5.3可以看出,采用风险比例为5%的“固定比例法”得到的最终结果与:“激进比例法"得到的结果相似。显而易见,与固定比例法相比,不断减少s值的做法并没有体现出太大优势,它的回撤甚至还要多。
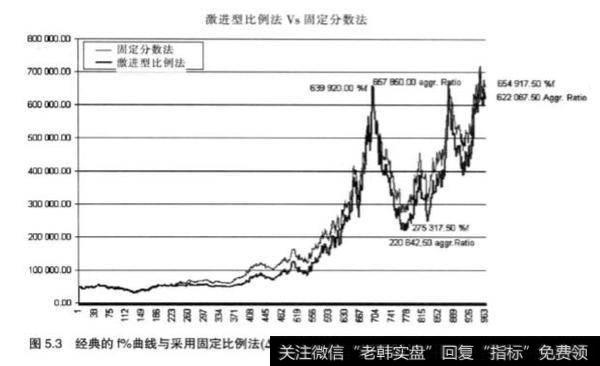
非对称比例法
在本书中,瑞恩.琼斯针对自己的方法提出了一个变量-非对称比例。 在这种方法中,他试图探究随着资金的增长或减少修改合约数的可能性。他最初的想法是,在资金减少的同时减少合约数,以此达到减少回撒的目的。
这种想法固然好,能够减小损失或使形势趋好,但又很难控制。每种方法首先都应该被测试,因为适合某个体系的方法未必适用于其他体系。
为了便于大家理解,我们假设琼斯将△值设定为5000欧元,初始资金为50000欧元。当资金达到55000欧元时,就买进第2份合约,达到65000欧元时买进第3 份合约。与此相对,当减小到65000欧元以下时,减少一份合约,即只买进2份合约;减少到55000欧元时,就只买进1份合约。而如果我们采用的是非对称法,就可以在资金降到60000欧元时只买进1份合约,这一数值刚好处于55000欧元和65000欧元之间。从我们对系统进行的测试来看,这一程序并不会给系统带来太多实际好处:回撤几乎与原来相同,而且最终结果还要略差一些。

图5.4是两种曲线的对比图:仅用肉眼就能发现,由于计算非常复杂,并未得出我们预期的结果。











