我们需要分析具体数据,并用其证实我们研发的理论。为此,我们要使用普通交易系统得到的结果,即我们要对建立在移动平均线交点上的系统结果进行分析。该系统是根据Forex中的欧元/美元汇率(每15分钟变动一次),其结果以美元作为计算单位,价格每次变动(每个tick) 12.5 美元,每笔交易中交易佣金和滑点之间的差值为20美元。系统由快速均线和慢速均线组成,正如图3.1中所描述的那样,当快速均线超过慢速均线时,系统就会选择买入;相反,当慢速均线超过快速均线时,系统就会选择卖出,同时将每份合约的止损额设定为1250美元。为了避免下午股市的剧烈波动,我们只考虑午夜到中午之间的汇率,并假设下午交易是停止的。为此,图中一般不含12 点以后的交易数据,就好像交易在中午突然停止,第二天上午再重新开盘一样。实际上,交易的实际亏损很可能超过设定的最大亏损额;将止损额设定为1250美元,会让人误以为亏损额会始终处于这一范围内,而忽略可能会出现较大浮动的半个交易日(下午)的变动,股市在第二天开盘后很可能会有非常大的浮动。

我们使用的工具显示了25个快速均线周期和40个慢速均线周期的良好表现。为了进一步限制该系统的投人数量,还要插人一个过滤器,只有在当日的最高值未超过前一天最高值的情况下,才可以保正它的长期进入(这里所说的最高值当然是午夜到正午之间所记录的最高值,因为超出这个时间范围的数值都不在我们的考虑范围之内)。反之亦然,只有在当日的最低值超过前一天最低值的情况下,它才可以保证短期进人。系统的操作性建立在市场趋势的基础上,而市场趋势正是由移动均线决定的:只要市场跨过平均线,并超过了前一天的最高值,信号就会失效,并且与短期趋势紧密相关。正因为如此,我们才插人上文所述的过滤器。为了让投资者对该系统有一个更加深入的了解,以下特别介绍该家统的一些简易语言代码(为了忽略下午的股市交易,我们只在图中选取了从午夜零点到中午12点之间的交易情况,欧洲中部时间)。
输入:慢速均线(40),快速均线(25).损失(1250);
如果快速均线(c)高于慢速均线(c),并且高线d(0)低于高线d(1)系统即买入:
如果快速均线(c)低于慢速均线(),并且高线d(0)高于高线d(1)系统即卖出;
终止合约设置;
正如你们所见,该系统非常平常,但它对我们的实践却非常有利。
笔者自2000年起就拥有自己的数据库,从2000年到2005 年年末,这个数据库经过了6年的测试期。
以下是该系统TradeStation报告中的一些信息(图3.2至图3.4)。可以发现,即便形势不是很好,这种方法仍然很有效。实际上,最大回撤数值大约是纯利润的1/4,这对于一些交易者来说是很难承受的。除了第一年非常困难(很多人或许都会放弃这-策略),系统在接下来还可能会遭受更多的损失。另外值得我们注意的是,系统遗受的最大损失将会远远超过预计的1250 美元。
这里得出的是仅仅操作一个合约的结果,从某种意义上来说,这些结果可以更加有趣。但是我们现在要看看,如果使用了我们之前学习过的某一种方法,又会出现什么结果呢?
本人想强调的是,这一系统的构成之所以没有遵循自身的传统标准,是因为它忽略了午后股市频繁交易的时间。这样做仅仅是为了向投资者展示一系列交易之后的资金管理效果,并非提供一些具体的操作性建议。

上一章中的凯利公式告诉我们应该投注资金的最优比例,但如何将这一理论应用到实际的交易系统中呢?
图3.2是我们获取的一些数据,“盈利率”一栏显示的是获利交易者的比例:也就是凯利公式中的获胜率W (用具体的数值来表示,而非百分数)。
“平均获胜1亏损率"则是平均获利额与亏损额的比率,即凯利公式中的R。以下就是凯利公式:
K%=(R+1)xW-1R我们现在来验证一-下:
W=0.4907(49.07%)
R=1.3248可以得到:
K%=(1.3248+1)x0.4907-1 =0.106265或10.6265%1.3248
这意味着,为了使获利最多,对于每一次交易,我们都应该投注总资金的10.6265%,这不难实现。因为一般情况下,从资金的操作性方面来说,你付出的代价就是你的赌本。而这里的交易是在副产品范围内进行的,投资数额是由单个衍生品所需的保证金决定的。
CME交易所的欧元/美元合约与此类似,我们假设保证金为2500美元,这就意味着只要你有2500美元,就能够买进1份欧元/美元合约。
然后呢?我们先看看手中的可用资金,再利用凯利公式计算应投注的资金,并以保证金的数额为单位,将它们分成若干份,就可以知道我们能移操作的合约数了。
在统计以上数据之前,我们先举一些例子。

假设我们有00000美元,利用凯利公式计算所得的最优比例为25%,那么应该投注的资金数额即为25000美元。如果每份合约的保证金为2500美元,那么利用25000美元的投注资金,我们就可以操作10份合约。
如果利用凯利公式计算得到的最优比例为20%,那么我们应该投注的资金就为20000美元,假设保证金为2500美元的话,我们就可以操作8份合约。
以上都只是近似计算,我们使用的方法相对保守,因为这样可以最大程度地降低风险。因此,如果我们拥有00000 美元,而凯利公式计算得出的最优比例为17%,那么我们就应该投注17000美元,17000/2500=6.8, 不能被2500整除,虽然6.8更接近于7,但我们仍要取6,所以在这种情况下,我们只能操作6份合约(后续我们将介绍如果取7的话会导致什么结果)。
因此,合约份数的计算公式如下:
合约数=in(本金x凯利值/保证金)这里的int代表“所得结果的整数部分"。
现在我们回到之前的例子,假设我们最初有50000美元。因此第一笔交易可操作2份合约,即:
合约数=in+(50000x0.106265/2500)-int(2.1253)=2
如果交易获胜的话,资金总额就会增长;反之,就会减少。这时就需要重新计算下一次交易可买进的合约数。
在我们所举的例子中,第一次交易获利642.5美元,因此,两份合约共获利1285美元,我们拥有的资金总额由最初的50000美元增长到51285美元。
合约数=in(51.285x0.106265/2.500)-int(2.1799)=2下一次应操作的合约数仍然为2,以此类推。
图3.6描述的是6年里进行的964次交易的情况。

细线描述的是使用所有可用资金操作1份合约的结果,由最初的50000美元增长到最终的138082.5 美元。实际上,图3.2中显示的获利额为88082.5美元,加上最初的50000美元,刚好是138082.5 美元。
而租线代表的是使用所有可用资金操作多份合约的结果,每次操作的合约数是根据凯利公式计算而来的。
可以发现,在一段较长的时间内,大概是整个交易时间的一半,使用凯利公式的结果甚至比未使用任何资金管理策略得到的结果还要差。但是后来,前者的情况有了很大好转,最终资金总额在6年末达到433090美元。
为什么在个别时期使用凯利公式的交易会比操作单个合约的交易结果更糟呢?想要解决这一问题,我们需要重点观察前几次的交易结果和资金表现(表3.1)。
从图3.7可以发现,如果包括计算结果的小数部分,最终得到的金额是807419.77美元,几乎是实际结果的2倍。

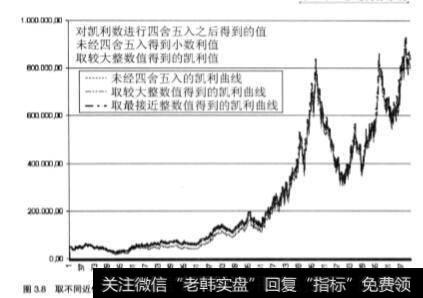
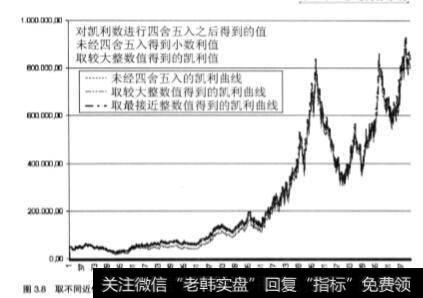
这一结果值得我们反思,是否应该舍去数字的小数部分,取较小整数值,还是取较大整数值,抑或取最接近的整数值,这些都是值得我们深思的问题。
图3.8是实际得到的凯利曲线,取较大整数值和取最接近数值(1.7的最接近整数为2,同样,如果是2.1,也取2)分别得到的凯利曲线图。实际上,用肉眼很难观察出三者的差别。
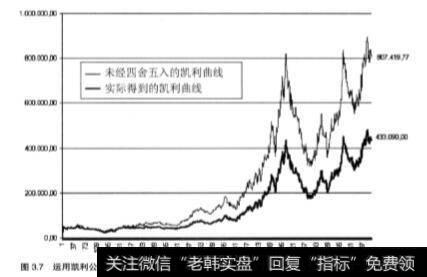
未进行任何四舍五入得到的最终结果是807419.77美元;取较大整数值的结果是798135美元;取最接近整数的结果是836130美元。
看似使用最后一种方法的结果最好,但这毕竟只是- .种理论假设,下面我们就来看看这一假设的荒谬之处。
如果将图3.5中的曲线与使用凯利公式的任意一个曲线做比较,不仅可以发现本金的扩大,而且还能看出资金的浮动。图3.6和图3.7也包含图3.5中的曲线,后者又被称为“原始曲线”。对比之后可以发现,相较于其他使用了凯利公式的曲线,原始曲线平缓且呈现一定的规律性。
如果我们从字面上理解并运用凯利公式(即舍去后面的小数部分),就能发现图3.9中几个非常有意思的地方:
第一个峰值是434040美元,接着资本严重缩水,急剧下降到175172.5美元;随即又达到一个新的峰值450957.5美元,继而又减少到301112.5美元。
说实话,我很怀疑,在股市如此的大起大落面前,有多少交易者还能够保持从容、镇定。因为他们永远不会知道,在低谷之后还会有一个新的峰值,我觉得即便是心理承受能力再大的人,也会有心理失衡的时候。


从图3.10中可以看出,取最接近整数值的结果所得的收益最大。这种情况下的最终收益的确非常可观,而随之而来的跌落也同样“令人失望”:
从80多万美元下跌到30多万美元,相信在这种“剧变”面前,没有哪个交易者还能够从容镇定地继续交易。
以上是使用50000美元操作的结果,下面我们来看看,如果将初始资金降低到30000美元,又会出现什么结果呢?
从图3.11中我们可以看出:中等粗细的线代表操作1份合约的情况,最细的线代表只取凯利结果中整数部分的走势图,而最粗的线则代表对凯利结果取最接近整数值的走势图。
这里的凯利曲线很奇怪,在最初一段不太清晰的变化之后它就一直停 留在23500美元的水平,而未使用任何资金管理方法的资金却增加了88082.5 美元(累计为1180825美元),对凯利结果取最接近整数值的最终资金为421245美元。
最初一段变化没有问题,我们奇怪的是,为什么它后来一直保持在23500美元的水平?主要因为最初的连续亏损使资金总额持续下降,最终下降到甚至连1份合约也买不了。
利用之前的公式就能得知:K%=0.106265利润=2500这时的剩余资金为23500美元。
合约数=int(23500>x0.106265/2500)=int(2497.2275/2500)=int(0.998891)=0

这就足以解释系统为什么会停止交易。从图3.12中可以看出,与上述不同的是取最接近整数值的情况,系统只能操作1份合约。
这时这种方法还是最好的吗?绝对不是。因为得到的结果可能小于0.5,如果取其最接近的整数就是0了。
值得注意的是,图3.12中的最初资金为25000美元而非30000美元。
初始资金减少了5000美元,细曲线与之前有所不同,而对于取最接近整数值的情况,在最初的一段亏损之后,也同样始终保持在11205美元的水平。
合约数=int(1 1205x0. 106265/2500)-=int(1 190.6993/2500)=int(0.47628)=0与上面的情况类似,系统同样停止了交易。
这还不是主要问题。众所周知,美国著名的期货交易员拉瑞.威廉姆斯就是凭借凯利公式在罗宾斯杯期货交易冠军赛中获得总冠军,他在不到一年的时间里使10000美元变成了110万美元。这一结果固然令人震惊,但同样还是拉瑞.威廉姆斯,在后来连续几次失利之后,果断地放弃了凯利公式。
主要原因在于,这种公式是根据系统的交易历史计算出某一阶段的百分比。将来的情况可能更好也可能更糟,如果将希望全部寄托于对系统表现的预计上,这未免过于冒险。
不要忘了,我们无法估计系统的最大损失(止损数额的设定完全是碰运气),使用凯利公式得到的平均亏损额同样不可靠。如前所述,如果将止损额设定为1250美元,但是从图3.4中可以看出,很多交易的亏损额都远远超过了这一数额。这是为什么呢?仔细分析这个图就可以发现,所有的交易都会在每天的00:15 (第一个价格柱的退出时间)早就退出。大盘的开启时间有中断,系统就无法严格按照设定的止损额进行交易。其实我们应该对这种情况早已司空见惯了,因此我们一定不能盲目轻信系统的理论最大亏损额。即便忽略大盘的中断因素,只使用一些资金管理技巧,实际损失额超过理论止损额的情况依然存在,因为发送给市场的指令可能会延迟或意外中断。在上一章中,我们已经见证了凯利比例是如何使利润最大化的,如果增加比例,得到的结果可能更糟;然而凯利公式毕竟只代表了一种有限的风险,它只能在有限的范围内起作用。
还需要强调的是,在最初-段时间里,我们对系统的特点也不是非常了解。如今,已经过去了6年,我们可以对该系统使用凯利公式或从报告中获取各种相关数据,这在6年前是不可能实现的。在这种情况下,要进行约20次交易,在之前的交易数据和信息基础上,再进行后续交易。很明显,这种方法的准确性不会很高。
建议那些认为凯利比例过于冒险的人,也可以使用其分数部分。但如果能研究出量化合约数的其他方法,才是最理想的。下一章我们将介绍几种最常用的方法,并分析它们各自的利弊,然后分别将其应用于我们的系统中,看看会得到什么结果。











