1、随机过程定义
一般来说,把一组随机变量定义为随机过程。在研究随机过程时人们透过表面的偶然性描述出必然的内在规律并以概率的形式来描述这些规律,从偶然中悟出必然正是这一学科的魅力所在。随机过程整个学科的理论基础是由柯尔莫哥洛夫和杜布奠定的。这一学科最早源于对随机过程物理学的研究,如吉布斯、玻尔兹曼、庞加莱等人对统计力学的研究,以及后来爱因斯坦、维纳、莱维等人对布朗运动的开创性工作。1907年前后,马尔可夫研究了一系列有特定相依性的随机变量,后人称之为马尔可夫链。1923年维纳给出布朗运动的数学定义,直到今天这一过程仍是重要的研究课题。随机过程一般理论的研究通常认为开始于20世纪30年代。1931年,柯尔莫哥洛夫发表了《概率论的解析方法》,1934年A·辛饮发表了《平稳过程的相关理论》,这两篇著作奠定了马尔可夫过程与平稳过程的理论基础。1953年,杜布出版了名著《随机过程论》,系统且严格地叙述了随机过程基本理论。
2、研究方法
研究随机过程的方法多种多样,主要可以分为两大类:一类是概率方法,其中用到轨道性质、随机微分方程等;另一类是分析的方法,其中用到测度论、微分方程、半群理论、函数堆和希尔伯特空间等,实际研究中常常两种方法并用。另外,组合方法和代数方法在某些特殊随机过程的研究中也有一定作用。研究的主要内容有:多指标随机过程、无穷质点与马尔可夫过程、概率随机过程与位势及各种特殊过程的专题讨论等。中国学者在平稳过程、马尔可夫过程、鞅论、极限定理、随机微分方程等方面做出了较好的成绩。
一个实际的随机过程是任意一个受概率支配的过程,例如,①看做是受孟德尔遗传学支配的群体的发展;②受分子碰撞影响的微观质点的布朗运动,或者是宏观空间的星体运动:③赌场中一系列的赌博;④公路一指定点汽车的通行。
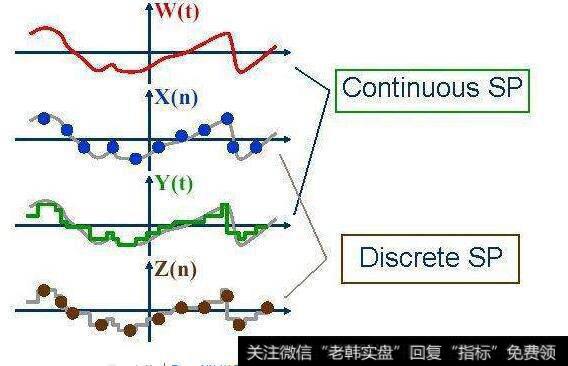
在每一种情形,一个随机系统在演化,这就是说它的状态随着时间而改变,于是,在时间t的状态具有偶然性,它是一个随机变量x(t),参数t的集通常是一个区间(连续参数的随机过程)或一个整数集合(离散参数的随机过程)。
如果系统的状态用一个数来表示,x(t)就是数值的,在其他情形,x(t)可以是向量值或者更为复杂。当状态变化时,它的值确定一个时间的函数:样本函数,支配过程的概率规律确定赋予样本函数的各种可能性质的概率。
数学上的随机过程是由实际随机过程概念引起的一种数学结构,人们研究这种过程,是因为它是实际随机过程的数学模型,或者是因为它的内在数学意义及它在概率论领域之外的应用。
数学上的随机过程可以简单地定义为一组随机变量,即指定一参数集,对于其中每一参数点I指定一个随机变量x(t).如果回忆起随机变量自身就是一个函数,以ω表示随机变量x(t)的定义域中的一点,并以x(t,ω)表示随机变量在ω的值,则随机过程就由刚才定义的x(t,ω)的函数及概率的分布完全确定。如果固定ω,这个二元函数就定义一个t的函数,即以x(t)表示的随机变量。如果固定ω这个二元函数就定义一个t的函数,这是过程的样本函数。
一个随机过程的概率分配通常是由指定它的随机变量的联合分布来给定的,这些联合分布及由它们诱导出来的概率可以解释为样本函数的性质的概率。例如,如果t0是一个参数值,样本函数在t0取正值的概率是随机变量x(t0)有正值的概率。在这个水平上的基本定理:任意指定的自身相容的联合概率分布对应一随机过程。
3。特殊随机过程
对过程的概率结构做各种假设,便得到各类特殊的随机过程。除正态过程、二阶过程外,重要的还有独立增量过程、马尔可夫过程、平稳过程、鞅点过程和分支过程等。贯穿这些过程类的有两个最重要、最基本的过程—布朗运动和泊松过程,它们的结构比较简单,便于研究且应用广泛。从它们出发,可以构造出许多其他过程。这两种过程的轨道性质不同,前者连续而后者则是上升的阶梯函数。
正如从普通函数发展到广义函数一样,随机过程也可发展到广义过程。设D为R上全体无穷次可微且支集有界的实值函数φ的集,定义在D上的连续线性泛函称为广义函数,全体广义函数的集记为Dx。考虑D×Ω上的二元函数x(φ,ω),如果对固定的ω,x(·,ω)∈Dx是广义函数,而对固定的φ,x(φ,·)是随机变量,则称{X(φ, ω):φ∈D}为定义在(Ω,F,P)上的广义过程。
据有穷维分布族的性质,也可以定义特殊的广义过程类,如广义平稳过程、广义正态过程等。例如,若对D中任意有限个线性独立函数φ1, φ2,…φn,有限维分布都是正态分布,则称x={x(φ,ω)}为广义正态过程。











