互换市场风险的测度
自从互换产生之日起,就有许多不同的方法对互换进行估值,而对互换交易市场风险的测度正是建立在对互换估值的基础上的。在 Andrew H. Chen和 Mohammed M. Chaudhury(1996)的一篇论文中是以无违约风险的零息票债券利率的期限结构为基石对互换进行估值并由此测定互换的市场风险。他们用零息票债券利率对互换的现金流贴现求得互换的价值,并证明决定零息票债券利率的基础经济变量及参数也可以决定互换的价值。
在这里,我们主要介绍另一种互换市场风险的测度方法Var方法。在一本关于var的开山之作中,P. Jorion是这样定义Var的:“Var是给定的置信水平和目标时段下预期的最大损失(或最坏情况下的损失)。”对于互换的市场风险,Var是指这样的种损失额,给定一概率水平v%及持有期t,在持有期内预计超过这一损失额的概率只有1-w%。在以下公式中,Var是指这样的数值,可能发生的概率(损失的绝对值>Var)<1-w%。例如,一个互换期限为1年,概率98%,Var100美元,其含义是该组合在一年中只有2%的时间里损失超过100美元。以利率互换为例。用Var测度市场风险的步骤有:
(1)确定了一个市场因素(r);
(2)确定修正持续期为线性a系数,用于度量以风险因素变动表现的风险;
(3)测度利率互换的风险;
Var计算,即在合意的百分位截止水平上计算风险因素的变动量。
首先,我们回忆一下利率互换的定价方法。
(一)互换的定价
在没有违约风险的情况下,利率互换可以通过分解方式定价即把利率互换看做在一只债券上保持多头,而在另一只债券上保持空头来进行定价。因此对于收入固定利率一方(相当于购买固定利率债券),互换的价值可以表示成:

其中,V是互换的价值,Bfix是浮动利率债券现值,Bflow是固定利率债券现值。
当合约签署时,V等于0,换句话说即协议之初浮动利率债券和固定利率债券的价值均等于0。在执行期间,该合约的价值可正可负。
(二)给风险因素和σ参数下定义
既然互换可以被视为一个债券组合,它的价值也就取决于市场利率r。
V=f(r) 11-2
为简单起见,我们假定收益率曲线是水平的,且只发生平移。因此,用于度量利率互换风险的惟一因素就是市场利率。下一步界定市场利率变动与互换利率变动的线性关系,适用以下公式

在Var方法中,σ参数扮演着很特殊的角色,通常表示一种资产价格的变动引起的另一种资产价格变动的线性近似估计。这里表示市场利率变动引起的互换价值变动的线性估计。债券价格变动和利率变动之间的关系可以通过修正的持续期线性表示出来。修正的持续期度量的债券价格随利率变动而发生的变化,也就是式(11-3)中的σ参数。附息债券的修正持续期按式(11-4)定义

其中,P代表债券的价格;dr代表利率的变化;D为“标准”的持续正如其创始人麦考利( Macauley)所定义的,持续期是债券现金流支付的加权期限,权重与每笔现金流的现值成比例。修正的持续期与持续期的区别如式(11-5)和式(11-6)所示

由于持续期是对风险的线性度量,证券组合的持续期就是各证券持续期的加权平均,如式(11-7)所示:

利率互换可以分解为一个债券的组合,因此,利率互换的持续期就是两只债券的持续期之和。
至此,计算利率互换的Var时已采取了两个额外的步骤
(1)确定了一个市场因素(r);
(2)确定修正持续期为线性a系数,用于度量以风险因素变动表现的风险。
(三)测度利率互换的风险
从定义修正持续期的公式(11-5),我们可以推导公式,用于近似估计利率变动引起的债券价格变化:

对接受固定利率一方,互换被视为一种固定利率债券并按此定价,类似地,对接受浮动利率的一方,互换也被视为一种浮动利率债券。固定利率债券特征使投资者在互换到期之前面临利率风险;从浮动利率方面来看,风险取决于浮动利率债券何时调整票面利率。如果票面利率连续调整,这一方面没有风险但由于票面利率是在离散时间段内调整的,所以,在任何给定时点上,浮动利率债券只能确定一个(下一个)票面利率。
这就是说,投资者在该项支付到期之前,都会面临利率风险。事实上,恰在调整票面利率之前,浮动利率债券的性质与公允价值等于本金的现金投资这一点上并无二致。刚刚调整之后,浮动利率债券就成为种短期固定利率债券。如果我们所考虑的时点恰是浮动利率债券行将调整票面利率之时,就不存在风险,因此,我们只考虑固定利率债券的风险。假设r小幅波动(因此,△r和△V可以分别被dr和dV取代),可以把公式(11-8)改写成

举例来说,一家公司和一家银行达成了互换协议,银行支付浮动利率现金流,而公司支付固定利率现金流。我们可以把互换当成同时进行的两笔交易来进行定价。
(1)公司借给银行一笔浮动利率资金。(2)银行借给公司同样数额一笔固定利率资金。从银行角度来看,利率互换是两只债券构成的组合,发行浮动利率的债券而同时购买固定利率债券。假设互换的固定利率支付计划按表11进行。假定水平的收益率曲线显示利率为4%,全部付款按年率4%进行。银行收到固定利率(即相当于银行“购买”了固定利率债券),这意味着,如果利率上升,固定利率债券的价值将下跌,反之将上涨。
表11-1接受固定利率一方的利率互换价值
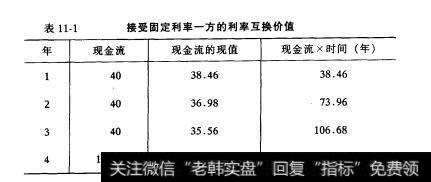
如前所述,我们只探讨互换的固定利率一方。为了度量固定利率一方的价值变动,我们必须正确计算参数(即修正持续期)。该计算如表11-2所示。
表11-2根据表11-1计算的价格和持续期

在0期,水平的收益率曲线显示利率为4%,固定利率债券价值1000(即互换的名义价值)。修正持续期为3.42年。用公式(11-8)就可以近似计算出接受固定利率的一方互换价值的变动情况。
在0期,我们用修正持续期来模拟相当于固定利率债券价值的变动。计算结果见表11-3,通过按新利率贴现所有现金流可以得出实际价格,用公式(11-8)计算的结果可倒求出预期价格。
表11-3固定收入证券模拟和实际价格变动
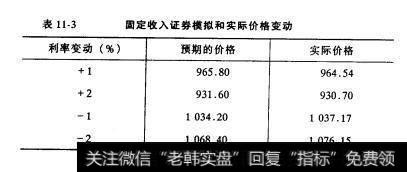
线性模型在近似计算收益率曲线平移导致的价格波动时相当有效。当我们模拟较大的变动(±2%)时,我们不要忘了公式(11-7)对计算微小的波动也是很起作用的。既然已假定浮动利率债券为零风险,我们就可以把固定利率一方的Var近似认为是整个互换的Var。
(四)Var计算
最后一个步骤是在合意的百分位截止水平上计算风险因素的变动量。该变动量可根据从过去总结的频率分布中推算得出,可通过假设利率波动服从某个已知的概率密度函数求得。假定1年期利率变动服从均值为0、标准差为0.5的正态分布,运用参数法,可计算出各概率水平的Var和1年期Var。计算过程见表11-4。
表11-4 1年期利率互换var

以上说明的是用va测度利率互换的市场风险,同样也可以用Var测度货币互换的市场风险。不同的是一个货币互换的价值是由互换涉及的两种货币各自的利率及两种货币的汇率等多因素决定的,这样货币互换的Ⅴar涉及多因素的联合概率密度分布。也可以用var测度商品互换或股权互换的市场风险,步骤与利率互换的市场风险测度相似,不同的是不同的互换决定其市场风险的因素不同。











